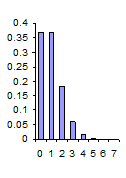
Αφίξεις – Κατανομή Poisson
Οι αφίξεις σε ένα σύστημα ουράς είναι οι «πελάτες» που προσέρχονται για εξυπηρέτηση. Τα χαρακτηριστικά των αφίξεων είναι:
- Το Μέγεθος του Πληθυσμού. Ο πληθυσμός των πελατών θεωρείται είτε άπειρος, ή πεπερασμένος. Στα πιο πολλά προβλήματα ο πληθυσμός του συστήματος είναι άπειρος.
- Η Κατανομή των Αφίξεων. Οι πελάτες φτάνουν στο σύστημα είτα με γνωστή σταθερή συχνότητα, ή σε τυχαίους χρόνους. Στη περίπτωση των τυχαίων αφίξεων μετράμε το μέσο αριθμό αφίξεων λ στη μονάδα του χρόνου και τις προσεγγίζουμε με τη στατιστική κατανομή Poisson.
Η ΚΑΤΑΝΟΜΗ POISSON
Όταν μας δίνεται ότι οι αφίξεις έχουν μέσο όρο λ ανά μονάδα χρόνου και ακολουθούν κατανομή Poisson, τότε μπορούμε να υπολογίσουμε τη πιθανότητα να έχουμε Χ (1, 2, …, λ, κλπ.) αφίξεις ανά μονάδα χρόνου από το τύπο:
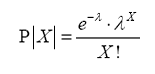
Για να γίνει πιο κατανοητός ο ρόλος της κατανομής Poisson παραθέτουμε τον παρακάτω πίνακα με τις τιμές και τα διαγράμματα για διάφορες τιμές των λ & Χ.
| Πιθανότητα Ρ|Χ|, για Χ Αφίξεις ανά Χρον. Μον. |
Μέσος Όρος Αφίξεων λ ανά Χρον. Μον. | ||
|---|---|---|---|
| λ=1 | λ=2 | λ=3 | |
| Ρ|Χ=0| | 0.367879 | 0.135335 | 0.049787 |
| Ρ|Χ=1| | 0.367879 | 0.270671 | 0.149361 |
| Ρ|Χ=2| | 0.183940 | 0.270671 | 0.224042 |
| Ρ|Χ=3| | 0.061313 | 0.180447 | 0.224042 |
| Ρ|Χ=4| | 0.015328 | 0.090224 | 0.168031 |
| Ρ|Χ=5| | 0.003066 | 0.036089 | 0.100819 |
| Ρ|Χ=6| | 0.000511 | 0.012030 | 0.050409 |
| Διάγραμμα Κατανομής Poisson |
|
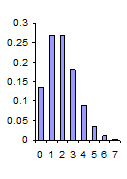 |
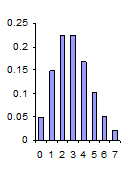 |
Από τις παραπάνω τιμές προκύπτει, για παράδειγμα, ότι:
- Αν έχουμε κατά μέσο όρο 2 αφίξεις την ώρα, η πιθανότητα να έρθουν 4 πελάτες είναι 9% (λ=2, Ρ|Χ=4|).
- Αν έχουμε κατά μέσο όρο 3 αφίξεις την ώρα, η πιθανότητα να μην έρθει κανένας είναι 5% (λ=3, Ρ|Χ=0|).
- Αν έχουμε κατά μέσο όρο 1 άφιξη την ώρα, η πιθανότητα να έρθουν 6 ή περισσότεροι πελάτες είναι σχεδόν 0% (λ=1, Ρ|Χ=6|).
Εξυπηρέτηση – Εκθετική Κατανομή
Οι πελάτες εξυπηρετούνται μέσα σε κάποιο χρονικό διάστημα από τις μονάδες εξυπηρέτησης. Τα χαρακτηριστικά του συστήματος εξυπηρέτησης είναι:
- Ο Χρόνος Εξυπηρέτησης. Ο χρόνος εξυπηρέτησης μπορεί είτε να είναι σταθερός, οπότε η εξυπηρέτηση γίνεται με σταθερή συχνότητα, ή όπως συμβαίνει συνήθως, να έχει τυχαίες διακυμάνσεις οπότε μετράμε το μέσο αριθμό πελατών μ που εξυπηρετούνται στη μονάδα του χρόνου και προσεγγίζουμε το χρόνο εξυπηρέτησης με την εκθετική κατανομή.
- Οι Μονάδες Εξυπηρέτησης. Μπορεί να υπάρχει: Α) μια μόνο μονάδα εξυπηρέτησης, οπότε οι πελάτες εξυπηρετούνται σειριακά, Β) πολλές παράλληλες μονάδες εξυπηρέτησης οπότε ο πελάτης εξυπηρετείται από τη πρώτη διαθέσιμη, Γ) πολλές διαδοχικές μονάδες εξυπηρέτησης οπότε ο πελάτης προσέρχεται διαδοχικά σε κάθε στάδιο.
Η ΕΚΘΕΤΙΚΗ ΚΑΤΑΝΟΜΗ
Όταν μας δίνεται ο μέσος αριθμός πελατών μ που εξυπηρετούνται ανά μονάδα χρόνου και ότι ο χρόνος εξυπηρέτησης ακολουθεί την Εκθετική κατανομή, τότε μπορούμε να υπολογίσουμε τη πιθανότητα ο χρόνος εξυπηρέτησης Τ να υπερβεί ένα δεδομένο χρόνο t από το τύπο:
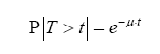
Για να γίνει πιο κατανοητός ο ρόλος της Εκθετικής κατανομής παραθέτουμε τον παρακάτω πίνακα με τις τιμές και τα διαγράμματα για διάφορες τιμές των μ & t.
| Πιθανότητα ο Χρ. Εξυπηρ. Τ να ξεπερνά τις t Χρον. Μον. |
Μέσος Όρος Πελατών μ που Εξυπηρετούνται ανά Χρον. Μον. | |
|---|---|---|
| μ=2/ώρα | μ=4/ώρα | |
| Ρ|Τ>0'| t =0 | 1 | 1 |
| Ρ|Τ>15'| t =0.25 | 0.513417 | 0.263597 |
| Ρ|Τ>30'| t =0.5 | 0.367879 | 0.135335 |
| Ρ|Τ>60'| t =1 | 0.135335 | 0.018316 |
| Ρ|Τ>90'| t =1.5 | 0.049787 | 0.002479 |
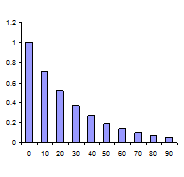
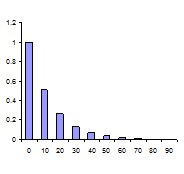
| Διαγράμματα Εκθετικής Κατανομής |
|
|
Από τις παραπάνω τιμές προκύπτει, για παράδειγμα, ότι:
- Αν εξυπηρετούνται κατά μέσο όρο 2 πελάτες την ώρα, η πιθανότητα να ξεπεράσει ο χρόνος εξυπηρέτησης τα 15' είναι 51%, ενώ η πιθανότητα να ξεπεράσει ο χρόνος εξυπηρέτησης τη 1.5 ώρα είναι μόνο 5% (μ=2, t=0.25 & t=1.5).
- Αν εξυπηρετούνται κατά μέσο όρο 4 πελάτες την ώρα, η πιθανότητα να ξεπεράσει ο χρόνος εξυπηρέτησης τα 15' είναι 26% (δηλ. με πιθανότητα 74% θα εξυπηρετηθούν εντός των 15'), ενώ η πιθανότητα να ξεπεράσει ο χρόνος εξυπηρέτησης τη 1.5 ώρα είναι σχεδόν 0% (μ=4, t=0.25 & t=1.5