Προβλήματα Μέγιστης Ροής Μεταξύ Δύο Κόμβων
Τα προβλήματα μέγιστης ροής τα συναντάμε συχνά σε δίκτυα μεταφοράς (transport networks). Ένα δίκτυο μεταφοράς είναι ένα γενικό μοντέλο με διαδρομές μεταφοράς υλικών, ρευστών, αυτοκινήτων, κεφαλαίων, ηλεκτρικού φορτίου, κλπ., από ένα κόμβο-αφετηρία σε ένα κόμβο-προορισμό. Οι κλάδοι ενός δικτύου μεταφοράς αντιπροσωπεύουν τη μέγιστη χωρητικότητα της διαδρομής από ένα κόμβο σε ένα άλλο την οποία δεν μπορεί να υπερβεί η μεταφερόμενη ποσότητα. Π.χ.: για ρευστά, οι κλάδοι θα είναι η μέγιστη παροχή των σωληνώσεων, για μεταφορές, το μέγιστο φορτίο, για συγκοινωνίες, οι μέγιστες θέσεις επιβατών, κ.λ.π.
Για παράδειγμα μια επιχείρηση προσπαθεί να μεταφέρει όλα τα προϊόντα της από το εργοστάσιο στο κεντρικό κατάστημα. Αν υπάρχουν διαφορετικοί δρόμοι και μέσα μεταφοράς πως μπορεί να τα συνδυάσει ώστε μεταφέρει το μεγαλύτερη δυνατή ποσότητα το συντομότερο δυνατό;
Οι Τομές Ενός Δικτύου και η Μέγιστη Ροή
Το πρόβλημα μέγιστης ροής είναι και αυτό ένα Π.Γ.Π. Η ειδική όμως δομή του επιτρέπει και εδώ την ανάπτυξη πιο αποτελεσματικών μεθόδων από τη Simplex, όπως είναι η μέθοδος Ford & Fulkerson που χρησιμοποιεί την έννοια της τομής ενός δικτύου.
Τομή ενός δικτύου μεταφοράς είναι μια τομή του γραφήματος η οποία διαχωρίζει την είσοδο από την έξοδο. Η χωρητικότητα μιας τομής είναι το άθροισμα των χωρητικοτήτων των κλάδων που τέμνει και που έχουν κατεύθυνση από την είσοδο προς την έξοδο (βλ. τομές A, B, C & D στο παρακάτω σχήμα.

Θεώρημα Μέγιστης Ροής και Ελάχιστης Τομής: Σε ένα δίκτυο μεταφοράς η μέγιστη τιμή της ροής είναι ίση με την ελάχιστη από τις χωρητικότητες όλων των δυνατών τομών του δικτύου.
Στη συνέχεια για διδακτικούς λόγους θα εξηγήσουμε τη μέθοδο επίλυσης (στη απλούστερη γραφική της μορφή και όχι στη συστηματοποιημένη μορφή με πίνακες), λύνοντας το παρακάτω πρόβλημα.
Το Πρόβλημα
Ένα δίκτυο αγωγών χρησιμοποιείται για τη μεταφορά υγρού μεταξύ 6 δεξαμενών. Έστω ότι προέκυψε η ανάγκη να μεταφερθούν τα περιεχόμενα της δεξαμενής 1 στη δεξαμενή 6 το ταχύτερο δυνατόν. Αν κάθε αγωγός έχει μια μέγιστη παροχή όπως αναγράφεται στο παρακάτω σχήμα, ποια θα είναι η μέγιστη ροή υγρού από τη δεξαμενή 1 στη δεξαμενή 6;
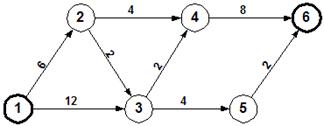
Επίλυση του Προβλήματος
Σε κάθε βήμα επιλέγουμε μια διαδρομή από την είσοδο έως την έξοδο και βρίσκουμε τη μέγιστη δυνατότητα ροής που έχει (δηλ. το κλάδο με τη μικρότερη χωρητικότητα). Αφαιρούμε τη ποσότητα από όλους τους κλάδους της διαδρομής και εφόσον υπάρχει περιθώριο προχωρούμε σε επιλογή άλλων διαδρομών.
ΕΠΑΝΑΛΗΨΕΙΣ
1ο ΒΗΜΑ
Επιλέγουμε τη διαδρομή 1-3-5-6. Η μέγιστη ροή της είναι 2 όση και του μικρότερου κλάδου της (5,6). Αφαιρούμε το 2 από τους άλλους δυο κλάδους και έχουμε:
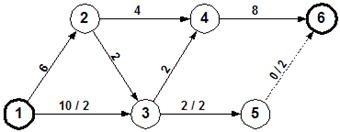
2ο ΒΗΜΑ
Επιλέγουμε τη διαδρομή 1-3-4-6. Η μέγιστη ροή της είναι 2 όση και του μικρότερου κλάδου της (3,4). Αφαιρούμε το 2 από τους άλλους δυο κλάδους και έχουμε:
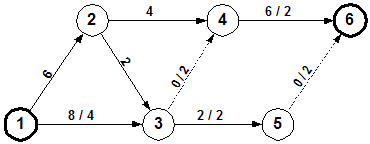
3ο ΒΗΜΑ
Επιλέγουμε τη διαδρομή 1-2-4-6. Η μέγιστη ροή της είναι 4 όση και του μικρότερου κλάδου της (2,4). Αφαιρούμε το 4 από τους άλλους δυο κλάδους και έχουμε:

Σε αυτό το σημείο δεν υπάρχει άλλη διαδρομή από το κόμβο 1 στο κόμβο 6 με θετική ροή. Η μέγιστη ροή είναι 6+2 = 8 και είναι ίση με την χωρητικότητα της τομής που περνά από τους τρεις κορεσμένους κλάδους (2,4), (3,4) & (5,6): 4+2+2 = 8.
ΠΑΡΑΔΕΙΓΜΑ
Δίνεται το παρακάτω δίκτυο μεταφοράς. Να υπολογισθεί η μέγιστη ροή από τον κόμβο 1 προς τον κόμβο 7.
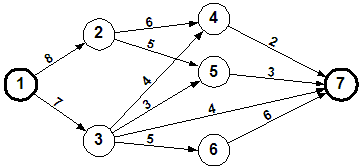
Λύση
Επιλέγουμε με τη σειρά τις διαδρομές: 1-2-4-7 (μεγ. ροή 2), 1-2-5-7 (μεγ. ροή 3), 1-3-6-7 (μεγ. ροή 5) και 1-3-7 (μεγ. ροή 2).
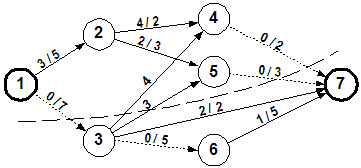
Η συνολική μέγιστη ροή προς το κόμβο 7 είναι 2+3+5+2 = 12.
Παρατηρούμε επίσης ότι η μέγιστη ροή είναι ίση με τη χωρητικότητα της τομής που διέρχεται από τους κλάδους (1,3), (5,7) & (4,7): 7+3+2 = 12 (οι άλλοι 2 κλάδοι (3,4) & (3,5) έχουν αντίθετη φορά).

