Προβλήματα Ελάχιστης (Συντομώτερης) Διαδρομής Μεταξύ Δύο Κόμβων

Τα προβλήματα προσδιορισμού της ελάχιστης διαδρομής (minimal path) με την οποία συνδέονται δυο κόμβοι ενός δικτύου είναι από τα σημαντικότερα στη θεωρία δικτύων.

Στα προβλήματα αυτά, ανάλογα πάντα με το ζητούμενο, οι κλάδοι αντιπροσωπεύουν τις αντίστοιχες μονάδες «κόστους» μετάβασης από τον κάθε κόμβο στους άλλους. Π.χ.: για ελάχιστη απόσταση, οι κλάδοι θα είναι χιλιομετρικές αποστάσεις, για ελάχιστο χρόνο, οι κλάδοι θα είναι απαιτούμενοι χρόνοι, για ελάχιστο κόστος, οι κλάδοι θα είναι χρηματικά ποσά, κ.λ.π.

Ένας προφανής τρόπος λύσης θα ήταν να υπολογίσουμε όλους τους πιθανούς συνδυασμούς διαδρομών με το συνολικό τους κόστος και να διαλέξουμε τον οικονομικότερο συνδυασμό. Ο τρόπος αυτός είναι όμως λειτουργικός μόνο για πολύ μικρά δίκτυα με λίγους (4-5) κόμβους και κλάδους.

Η συστηματική μέθοδος, αντίθετα, πρέπει να μπορεί να επιλύει και προβλήματα με εκατοντάδες κόμβους και χιλιάδες κλάδους. Η μέθοδος υπολογίζει τις ελάχιστες διαδρομές από το κόμβο εισόδου προς όλους τους υπόλοιπους κόμβους του δικτύου. Εμείς επιλέγουμε σαν λύση τη ελάχιστη διαδρομή για το κόμβο που μας ενδιαφέρει.

Για να εξηγήσουμε καλύτερα τη λειτουργία αυτής της μεθόδου βελτιστοποίησης για ελάχιστες διαδρομές, θα λύσουμε το παρακάτω πρόβλημα.

Το Πρόβλημα

Το οδικό δίκτυο μιας πόλης προσφέρει έναν μεγάλο αριθμό εναλλακτικών διαδρομών. Έστω ότι ένα όχημα (π.χ. ασθενοφόρο) βρίσκεται στο άκρο Α και πρέπει να φτάσει όσο γίνεται συντομότερα στο άλλο άκρο Β (π.χ. στο νοσοκομείο). Ποια είναι η συντομότερη διαδρομή που πρέπει να ακολουθήσει;

Το κύριο οδικό δίκτυο της πόλης με το «κόστος» (π.χ. καθυστέρηση, απόσταση, κλπ.) κάθε κλάδου φαίνεται στο επόμενο σχήμα:

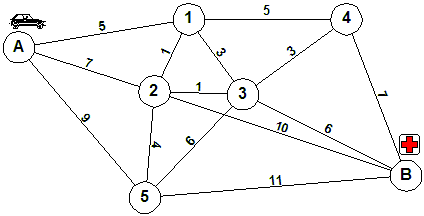
Επίλυση του Προβλήματος

Ζητείται να βρεθεί η ελάχιστη διαδρομή μεταξύ των δυο κόμβων (Α) και (Β).

ΑΡΧΙΚΟ ΒΗΜΑ

Δημιουργούμε ένα πίνακα και στη πρώτη σειρά βάζουμε όλους τους κόμβους του δικτύου. Κάτω από κάθε κόμβο καταγράφουμε όλους τους κλάδους που ξεκινούν από αυτόν σε αύξουσα σειρά κόστους.

Δεν καταγράφουμε τους κλάδους που αναχωρούν από το κόμβο προορισμού (Β) ή καταλήγουν στο κόμβο αναχώρησης (Α), δηλ., αυτούς που είναι εκ των πραγμάτων αντίθετοι με τη πορεία που θα ακολουθήσουμε.

Είσοδος
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

Ξεκινούμε τα επαναληπτικά βήματα από τον κόμβο εκκίνησης Α.

ΕΠΑΝΑΛΗΨΕΙΣ

1ο ΒΗΜΑ

1. Βρίσκουμε τους πλησιέστερους στον Α κόμβους. Είναι ο κόμβος 1 μέσω του κλάδου (Α,1).
2. Μαρκάρουμε τον παραπάνω κλάδο και γράφουμε πάνω από τη στήλη του κόμβου 1 το κόστος του (απόσταση) από τον Α: (Α,1)=5.
3. Διαγράφουμε όλους τους άλλους κλάδους που οδηγούν στον κόμβο 1 (δηλ τους: (2,1), (3,1) & (4,1) ).

Είσοδος	+5
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

2ο ΒΗΜΑ

1. Βρίσκουμε τους πλησιέστερους στους Α & 1, κόμβους. Είναι ο κόμβος 2 με τους κλάδους (Α,2) & (1,2) και συνολικά πλησιέστερος μέσω του κλάδου (1,2) (1+5<7).
2. Μαρκάρουμε τον παραπάνω κλάδο και γράφουμε πάνω από τη στήλη του 2 το κόστος του (απόσταση) από τον Α: (Α,1)+(1,2) = 5+1 = 6.
3. Διαγράφουμε όλους τους άλλους κλάδους που οδηγούν στον κόμβο 2 (δηλ τους: (Α,2), (3,2) & (5,2) ).

Είσοδος	+5	+6
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

3ο ΒΗΜΑ

1. Βρίσκουμε τους πλησιέστερους στους Α, 1 & 2, κόμβους. Είναι ο κόμβος 5 με τον κλάδο (Α,5) και ο 3 με τους (1,3) & (2,3). Συνολικά πλησιέστερος είναι ο 3 μέσω του κλάδου (2,3) (1+6<3+5<9).
2. Μαρκάρουμε τον παραπάνω κλάδο και γράφουμε πάνω από τη στήλη του 3 το κόστος του (απόσταση) από τον Α: (Α,1)+(1,2)+(2,3) = 5+1+1 = 7.
3. Διαγράφουμε όλους τους άλλους κλάδους που οδηγούν στον κόμβο 3 (δηλ τους: (1,3), (4,3) & (5,3) ).

Είσοδος	+5	+6	+7
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

4ο ΒΗΜΑ

1. Βρίσκουμε τους πλησιέστερους στους Α, 1, 2 & 3, κόμβους. Είναι ο κόμβος 5 με τους κλάδους (Α,5) & (2,5) και ο 4 με τους (1,4) & (3,4). Συνολικά πλησιέστερος είναι ο 5 μέσω του κλάδου (Α,5) (9<4+6<5+5<4+7).
2. Μαρκάρουμε τον παραπάνω κλάδο και γράφουμε πάνω από τη στήλη του 5 το κόστος του (απόσταση) από τον Α: (Α,5) = 9.
3. Διαγράφουμε όλους τους άλλους κλάδους που οδηγούν στον κόμβο 5 (δηλ τους: (2,5) & (3,5) ).

Είσοδος	+5	+6	+7		+9
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

5ο ΒΗΜΑ

1. Βρίσκουμε τους πλησιέστερους στους Α, 1, 2, 3 & 5, κόμβους. Είναι ο κόμβος 4 με τους κλάδους (1,4) & (3,4) και ο Β με τους (2,Β) & (5,Β). Συνολικά πλησιέστερος είναι ο 4 μέσω του κλάδου (1,4) (5+5<4+7<10+6<11+9).
2. Μαρκάρουμε τον παραπάνω κλάδο και γράφουμε πάνω από τη στήλη του 4 το κόστος του (απόσταση) από τον Α: (Α,1)+(1,4) = 5+5 = 10.
3. Διαγράφουμε όλους τους άλλους κλάδους που οδηγούν στον κόμβο 4 (δηλ τον: (3,4) ).

Είσοδος	+5	+6	+7	+10	+9
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

6ο ΒΗΜΑ (Τελικό)

1. Βρίσκουμε τους πλησιέστερους στους Α, 1, 2, 3, 4 & 5, κόμβους. Είναι ο κόμβος Β με τους κλάδους (2,Β), (3,Β), (4,Β) & (5,Β). Συνολικά πλησιέστερος είναι ο Β μέσω του κλάδου (3,Β) (6+7<10+6<7+10<11+9).
2. Μαρκάρουμε τον παραπάνω κλάδο και γράφουμε πάνω από τη στήλη του Β το κόστος του (απόσταση) από τον Α: 6+7 = 13.
3. Διαγράφουμε όλους τους άλλους κλάδους που οδηγούν στον κόμβο Β (δηλ τον: (2,Β), (4,Β) & (5,Β) ).

Είσοδος	+5	+6	+7	+10	+9	+13
Α	1	2	3	4	5	Β
(Α,1) 5	(1,2) 1	(2,1) 1	(3,2) 1	(4,3) 3	(5,2) 4
(Α,2) 7	(1,3) 3	(2,3) 1	(3,1) 3	(4,1) 5	(5,3) 6
(Α,5) 9	(1,4) 5	(2,5) 4	(3,4) 4	(4,Β) 7	(5,Β) 11
		(2,Β) 10	(3,5) 6
			(3,Β) 6

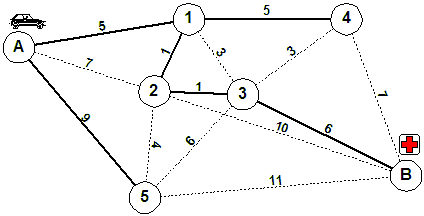
Η τελική λύση μας δίνει όλες τις ελάχιστες διαδρομές με το συνολικό κόστος τους, για κάθε κόμβο του δικτύου, ξεκινώντας από τον κόμβο Α. Για να βρούμε τη διαδρομή που μας ενδιαφέρει, ξεκινάμε από τον τελικό κόμβο (Β) και ακολουθούμε τους επιλεγμένους κλάδους που οδηγούν στην αρχή (Α).

Για το συγκεκριμένο πρόβλημα η λύση είναι η διαδρομή Α–1–2–3–Β, από τους κλάδους (Α,1)-(1,2)-(2,3)-(3,Β) και η οποία είναι η συντομότερη και έχει συνολικό «κόστος» 5+1+1+6 = 13.

 

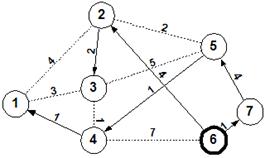
ΠΑΡΑΔΕΙΓΜΑ

Δίνεται το παρακάτω δίκτυο.

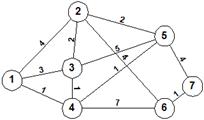
Α) Να βρεθεί η συντομότερη διαδρομή αν ο κόμβος εισόδου είναι ο 1 και ο κόμβος εξόδου είναι ο 7.

Ο τελικός πίνακας και οι διαδρομές είναι:

Είσοδος	+4	+2	+1	+2	+9	+6
1	2	3	4	5	6	7
(1,4) 1	(2,3) 2	(3,4) 1	(4,3) 1	(5,4) 1	(6,7) 1
(1,3) 3	(2,5) 2	(3,2) 2	(4,5) 1	(5,2) 2	(6,2) 4
(1,2) 4	(2,6) 5	(3,5) 5	(4,6) 7	(5,7) 4	(6,4) 7
				(5,3) 5

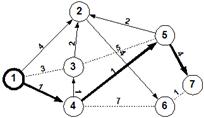
Η συντομότερη διαδρομή από τον 1 στον 7 είναι η (1-4-5-7) = 6. Παρατηρούμε επίσης ότι για το κόμβο 2 υπάρχουν 3 ισοδύναμες διαδρομές (1-2) = (1-4-3-2) = (1-4-5-2) = 4.

Β) Να βρεθούν οι συντομότερες διαδρομές των υπολοίπων κόμβων αν ο κόμβος εισόδου είναι ο 6.

Ο τελικός πίνακας και οι διαδρομές είναι:

+7	+4	+6	+6	+5	Είσοδος	+1
1	2	3	4	5	6	7
(1,4) 1	(2,3) 2	(3,4) 1	(4,1) 1	(5,4) 1	(6,7) 1	(7,5) 4
(1,3) 3	(2,5) 2	(3,2) 2	(4,3) 1	(5,2) 2	(6,2) 4
(1,2) 4	(2,1) 4	(3,1) 3	(4,5) 1	(5,7) 4	(6,4) 7
		(3,5) 5		(5,3) 5

 

<<Προηγ. | ΤΜΗΜΑ | Επόμ.>>

------

Σημείωση: Ο Δικτυακός Τόπος είναι υπό κατασκευή και συνεχή επέκταση και βελτίωση. Η αρχική του μορφή αναπτύχθηκε στα πλαίσια του προγράμματος ΕΠΕΑΕΚ ΙΙ - "Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών" του Τμήματος Πολιτικών Έργων Υποδομής του ΤΕΙ Αθήνας.