Προβλήματα Βέλτιστης ή Ελάχιστης Κάλυψης Όλων των Κόμβων
Τα προβλήματα ελαχιστοποίησης της κάλυψης όλων των κόμβων ενός δικτύου συναντώνται πολύ συχνά σε εργασίες υποδομής. Για παράδειγμα όταν σε ένα οικισμό πρέπει να εγκατασταθεί δίκτυο ύδρευσης σε όλες τις κατοικίες, ποια διαδρομή θα χρειαστεί το ελάχιστο κόστος σωληνώσεων και εκσκαφών; Όταν σε μια αγροτική περιοχή σχεδιάζεται η οδική σύνδεση απομονωμένων αγροικιών, ποια είναι η συντομότερη ή οικονομικότερη διαδρομή που μπορεί να χαραχτεί; Τα ίδια ερωτήματα τίθενται και στη σχεδίαση δικτύων ηλεκτροδότησης, τηλεφωνικών δικτύων, δικτύων Η/Υ, και άλλων δικτύων μεταφοράς και διανομής.
Και σε αυτά τα προβλήματα, ανάλογα πάντα με το ζητούμενο, οι κλάδοι αντιπροσωπεύουν τις αντίστοιχες μονάδες «κόστους» μετάβασης από τον κάθε κόμβο στους άλλους. Π.χ.: για ελάχιστη απόσταση, οι κλάδοι θα είναι χιλιομετρικές αποστάσεις, για ελάχιστο χρόνο, οι κλάδοι θα είναι απαιτούμενοι χρόνοι, για ελάχιστο κόστος, οι κλάδοι θα είναι χρηματικά ποσά, κ.λ.π.
Η μέθοδος επίλυσης είναι σχετικά απλή. Πρώτα διατάσσουμε όλους τους κλάδους του δικτύου κατά αύξουσα σειρά «κόστους» (αν 2 κλάδοι είναι ίσοι δεν έχει σημασία η σειρά), και στη συνέχεια επιλέγουμε με τη σειρά από τον μικρότερο προς το μεγαλύτερο όσους κλάδους δεν δημιουργούν κλειστό βρόγχο (δηλ. δεν επιστρέφουν σε κόμβο που έχει ήδη συνδεθεί).
Για να εξηγήσουμε καλύτερα τη λειτουργία της μεθόδου βέλτιστης κάλυψης, θα λύσουμε το παρακάτω πρόβλημα.
Το Πρόβλημα
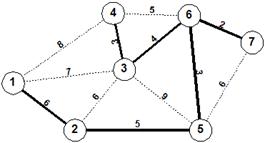
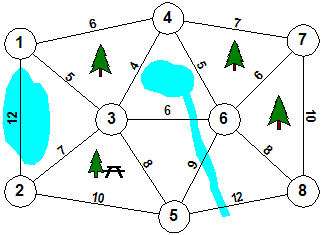
Μια ομάδα εξοχικών κατοικιών πρόκειται να υδροδοτηθεί. Οι απαιτούμενες εργασίες και υλικά με βάση την απόσταση και το έδαφος έχουν υπολογιστεί σε χιλιάδες € και δίνονται στο παρακάτω σχήμα όπου, κάθε κλάδος αντιπροσωπεύει το κόστος σύνδεσης δυο κόμβων (κατοικιών). Ποια είναι η οικονομικότερη κάλυψη υδροδότησης όλων των κατοικιών;
Επίλυση του Προβλήματος
Ζητείται να βρεθεί η ελάχιστη κάλυψη όλων των κόμβων του δικτύου.
ΑΡΧΙΚΟ ΒΗΜΑ
Δημιουργούμε ένα πίνακα και καταγράφουμε όλους τους κλάδους του δικτύου σε αύξουσα σειρά κόστους.
| α/α | Κλάδος | «Κόστος» | ΕΠΙΛΟΓΗ |
| 1 | (3,4) | 4 | Ναι |
| 2 | (4,6) | 5 | Ναι |
| 3 | (1,3) | 5 | Ναι |
| 4 | (1,4) | 6 | Όχι – κλείνει βρόγχο |
| 5 | (3,6) | 6 | Όχι – κλείνει βρόγχο |
| 6 | (6,7) | 6 | Ναι |
| 7 | (2,3) | 7 | Ναι |
| 8 | (4,7) | 7 | Όχι – κλείνει βρόγχο |
| 9 | (6,8) | 8 | Ναι |
| 10 | (3,5) | 8 | Ναι |
| 11 | (5,6) | 9 | Όχι – κλείνει βρόγχο |
| 12 | (2,5) | 10 | Όχι – κλείνει βρόγχο |
| 13 | (7,8) | 10 | Όχι – κλείνει βρόγχο |
| 14 | (5,8) | 12 | Όχι – κλείνει βρόγχο |
| 15 | (1,2) | 12 | Όχι – κλείνει βρόγχο |
ΒΗΜΑΤΑ ΕΠΙΛΟΓΗΣ
- Επιλέγουμε τον 1ο, 2ο & 3ο κατά σειρά κλάδο (3,4), (4,6) & (1,3).
- Δεν επιλέγουμε τον 4ο & 5ο κλάδο (1,4) & (3,6) γιατί κλείνουν βρόγχο.
- Επιλέγουμε τον 6ο & 7ο κατά σειρά κλάδο (6,7) & (2,3).
- Δεν επιλέγουμε τον 8ο κλάδο (4,7) γιατί κλείνει βρόγχο.
- Επιλέγουμε τον 9ο & 10ο κατά σειρά κλάδο (6,8) & (3,5).
- Δεν επιλέγουμε τους υπόλοιπους κλάδους γιατί κλείνουν βρόγχο.
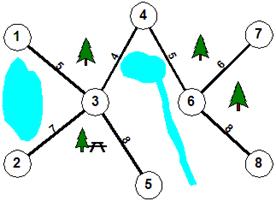
Το τελικό δίκτυο ύδρευσης, με την οικονομικότερη κάλυψη όλων των κατοικιών (43 χιλιάδες €), είναι το παρακάτω:
ΠΑΡΑΔΕΙΓΜΑ
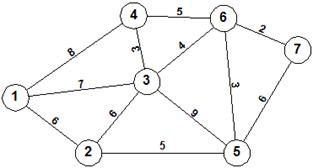
Επτά (7) περιοχές θα συνδεθούν με αγροτικές οδούς. Οι αποστάσεις μεταξύ των περιοχών δίνονται στο παρακάτω σχήμα (δίκτυο) όπου, κάθε κλάδος αντιπροσωπεύει χιλιομετρικές αποστάσεις. Ποια είναι η συντομότερη οδική κάλυψη όλων των περιοχών;
| α/α | Κλάδος | «Κόστος» | ΕΠΙΛΟΓΗ |
| 1 | (6,7) | 2 | Ναι |
| 2 | (3,4) | 3 | Ναι |
| 3 | (6,5) | 3 | Ναι |
| 4 | (3,6) | 4 | Ναι |
| 5 | (4,6) | 5 | Όχι |
| 6 | (2,5) | 5 | Ναι |
| 7 | (5,7) | 6 | Όχι |
| 8 | (2,3) | 6 | Όχι |
| 9 | (1,2) | 6 | Ναι |
| 10 | (1,3) | 7 | Όχι |
| 11 | (1,4) | 8 | Όχι |
| 12 | (3,5) | 9 | Όχι |