Μέθοδοι Επίλυσης

1. Ξεκινάμε την επίλυση με την εύρεση μιας αρχικής βασικής λύσης χρησιμοποιώντας τη μέθοδο Ελάχιστου Πίνακα (μια από τις πολλές μεθόδους, άλλες μέθοδοι είναι οι: Vogel, ΒΔ γωνίας, κλπ.)
2. Έχοντας την αρχική βασική λύση βρίσκουμε τη βέλτιστη με τη μέθοδο Stepping-Stone.

Η διαδικασία των μεθόδων εξηγείται εύκολα με το παράδειγμα που ακολουθεί

Επίλυση του Προβλήματος

Έστω ότι συμπληρώθηκε ο προηγούμενος πίνακας με τα δεδομένα ενός προβλήματος και προέκυψε ο παρακάτω για επίλυση, δηλ. την εύρεση των βέλτιστων τιμών των Xij:

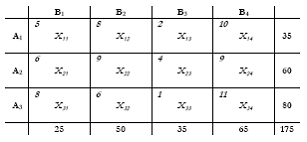
ΑΡΧΙΚΗ ΛΥΣΗ – ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΟΥ ΠΙΝΑΚΑ

Η μέθοδος ξεκινά από το μικρότερο Cij του πίνακα και δίνοντας στο Xij τιμή ίση με το ελάχιστο των αi & βj. Μετά προχωρά προς τα αμέσως μεγαλύτερα επαναλαμβάνοντας τη διαδικασία.

1. Το μικρότερο Cij του πίνακα είναι το (3,3), δίνουμε στο X33 σαν τιμή το ελάχιστο των α3 & β3, δηλ.: min(80, 35) = 35. Εφόσον είναι ίσο με το β3 τα υπόλοιπα Χ της στήλης του θα είναι μηδέν, γι’ αυτο διαγράφουμε τα (1,3) & (2,3).
2. Το επόμενο μικρότερο Cij του πίνακα είναι το (1,1), κάνουμε το X11 = min(25, 35) = 25, και διαγράφουμε τα (2,1) & (3,1).

Ο πίνακας τώρα έχει την εξής μορφή:

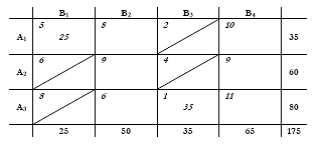
1. Το επόμενο μικρότερο Cij του πίνακα είναι το (3,2), κάνουμε το X32 = min(80-35, 50) = 45, και διαγράφουμε το (3,4).
2. Το επόμενο μικρότερο Cij του πίνακα είναι το (1,2), κάνουμε το X12 = min(50-45, 35-25) = 5, και διαγράφουμε το (2,2).
3. Τέλος, δίνουμε τιμές και στα X24 = 60 & X14 = 5.

Ο τελικό πίνακας τώρα έχει την εξής μορφή, η οποία αποτελεί την αρχική βασική λύση:

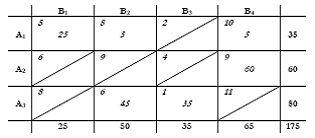
Το συνολικό κόστος των μεταφορών στην αρχική αυτή λύση θα είναι:
5·25+8·5+10·5+9·60+6·45+1·35 = 1060.

Από τις 12 μεταβλητές Xij, οι 6 έχουν πάρει τιμή και είναι οι βασικές μεταβλητές ενώ οι υπόλοιπες που διαγράφηκαν δεν περιλαμβάνονται στις β.μ.

ΒΕΛΤΙΣΤΗ ΛΥΣΗ – ΜΕΘΟΔΟΣ STEPPING-STONE

Όπως και με τη Simplex, η μέθοδος αναζητά μια καλύτερη λύση με το να εισάγει στις β.μ. μια από τις μη β.μ.

Για να επιλέξει μια μεταβλητή θα πρέπει αυτή φυσικά να συνεισφέρει στη μείωση του κόστους.

Η μέθοδος λοιπόν ξεκινά ελέγχοντας όλες τις μη β.μ. (αυτές δηλ. που διαγράφηκαν στην αρχική) για το πώς και πόσο θα επηρεάσουν το συνολικό κόστος αν τις αυξήσουμε κατά μια (1) μονάδα. (Σημ.: οι αρχικές λύσεις σημειώνονται με κύκλο για να ξεχωρίζουν).

Αρχίζοντας από το (1,3), αν αυξηθεί κατά +1, για να τηρηθούν οι περιορισμοί, το (3,3) θα μειωθεί (-1), το (3,2) θα αυξηθεί (+1) και το (1,2) θα μειωθεί (-1).

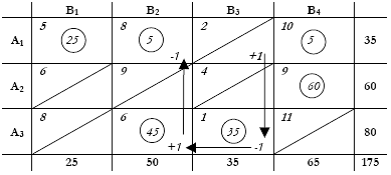
Η συνολική οριακή επίδραση στο κόστος αν αυξηθεί η Χ13 κατά 1 μονάδα θα είναι: c13 = +1·2 -1·1 +1·6 -1·8 = 2-1+6-8 = -1. Άρα, η είσοδος της Χ13 στις β.μ. βοηθάει, κατ’ αρχήν, στη μείωση του κόστους. Γράφουμε το c13 = -1 στο κελί (1,3) και συνεχίζουμε με τις όλες τις άλλες μη β.μ.: c21 = +6-9+10-5 = +2, c22 = +9-9+10-8 = +2, c23 = +4-9+10-8+6-1 = +2, c31 = +8-6+8-5 = +5, c33 = +11-10+8-6 = +3, οπότε και προκύπτει ο παρακάτω πίνακας όπου φαίνεται ότι μόνο η (1,3) μπορεί να συνεισφέρει στη μείωση του κόστους.

Για να βρούμε τη νέα λύση, δίνουμε στη Χ13 τη μικρότερη από τις γειτονικές τιμές στο βρόγχο υπολογισμού του c13 (γραμμή 1 ή στήλη 3), έτσι ώστε η Χ13 να αντικαταστήσει πλήρως την αντίστοιχη β.μ. (Χ12). Τέλος, ρυθμίζουμε και τις υπόλοιπες β.μ. του βρόγχου (Χ32 & Χ33).

Η νέα λύση δίνεται στον παρακάτω πίνακα:

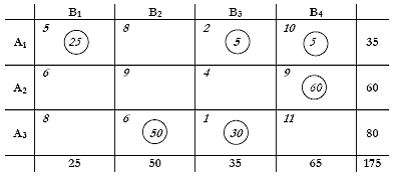
Επαναλαμβάνουμε τον έλεγχο των μη β.μ. υπολογίζοντας την οριακή επίδραση τους στο κόστος αν αυξηθούν κατά 1 μονάδα. Διαπιστώνουμε  ότι όλα τα αποτελέσματα είναι θετικά, άρα, καμία δεν μπορεί να βοηθήσει στη μείωση του κόστους.

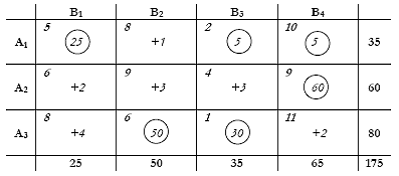
Η λύση αυτή είναι, επομένως, η βέλτιστη και θα έχει συνολικό κόστος:
5·25+2·5+10·5+9·60+6·50+1·30 = 1055.

<<Προηγ. | ΤΜΗΜΑ | Επόμ.>>

------

Σημείωση: Ο Δικτυακός Τόπος είναι υπό κατασκευή και συνεχή επέκταση και βελτίωση. Η αρχική του μορφή αναπτύχθηκε στα πλαίσια του προγράμματος ΕΠΕΑΕΚ ΙΙ - "Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών" του Τμήματος Πολιτικών Έργων Υποδομής του ΤΕΙ Αθήνας.