Παράδειγμα: Το Πρόβλημα Μεταφοράς της εταιρείας «Τσιμέντα ΑΕ»
Η εταιρεία έχει 3 εργοστάσια τσιμέντου τα Α1, Α2 και Α3, που παράγουν 600, 900 & 1000 τόνους το μήνα αντίστοιχα.
Η εταιρεία θα προμηθεύσει 3 μεγάλα εργοτάξια τα Β1, Β2 και Β3 τα οποία χρειάζονται 1000, 1000 & 400 τόνους αντίστοιχα.
Η αποστάσεις εργοστασίων και εργοταξίων και το κόστος μεταφοράς φαίνονται στο σχήμα που ακολουθεί.

Κόστος των μεταφορών ανά μονάδα προϊόντος από τα εργοστάσια στα εργοτάξια.
Ζητείται να βρεθεί ο οικονομικότερος τρόπος μεταφοράς για τον επόμενο μήνα καθώς και όποια άλλη οικονομία μπορεί να γίνει στη παραγωγή.
ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ
Το πρόβλημα διαφέρει ελαφρά από το τυπικό πρόβλημα μεταφοράς στο ότι οι προσφερόμενες και ζητούμενες ποσότητες δεν είναι ίδιες. Εδώ, η παραγόμενη ποσότητα είναι περισσότερη από τη ζήτηση.
Για να το αντιμετωπίσουμε προσθέτουμε άλλη μία περιθωριακή μεταβλητή S στις Β η οποία θα αφορά τη ποσότητα του προϊόντος που θα παραμείνει στα εργοστάσια. Το κόστος μεταφοράς στην S θα είναι 0 και η «ζήτηση» της S θα είναι η πλεονάζουσα παραγωγή δηλ. η διαφορά: ΣΑi – ΣΒj = 2500 - 2400 = 100 τ.
Επίλυση Του Προβλήματος
Τοποθετούμε τα δεδομένα (Αi ,Βj ,& Cij) στον παρακάτω πίνακα:
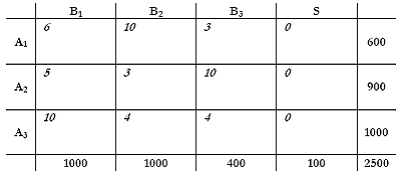
ΑΡΧΙΚΗ ΛΥΣΗ – ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΟΥ ΠΙΝΑΚΑ
Με τη μέθοδο του ελάχιστου πίνακα βρίσκουμε μια αρχική βασική λύση με τη παρακάτω σειρά (αρχίζοντας από το μικρότερο Cij εκτός του 0):
C22 = 3, Χ22 = min{900, 1000}= 900 & διαγράφονται τα: Χ21 , Χ23 , Χ24.
C13 = 3, Χ22 = min{600, 400} = 400, & διαγράφεται το: Χ33.
C32 = 4, Χ32 = min{1000, 1000-900} = 100, & διαγράφεται το: Χ12.
C11 = 6, Χ11 = min{600-400, 1000} = 200, & διαγράφεται το: Χ14.
C31 = 10, Χ31 = min{1000-100, 1000-200} = 800.
Και τέλος, Χ31 = 100.
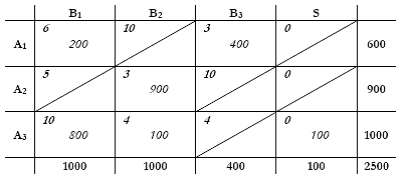
Το συνολικό κόστος της αρχικής λύσης είναι:
6·200+3·400+3·900+10·800+4·100+0·100 = 13500.
ΒΕΛΤΙΣΤΗ ΛΥΣΗ – ΜΕΘΟΔΟΣ STEPPING-STONE
Ξεκινώντας από τη παραπάνω αρχική λύση, βρίσκουμε για όλες τις μη β.μ. την οριακή επίδραση τους στο κόστος αν αυξηθούν κατά 1 μονάδα: c12 =+10-9+10-4= +10, c14 =+0-6+10-0= +4, c21 =+5-10+4-3= -4, c23 =+10-3+6-10+4-3= +4, c24 =+0-3+4-0= +1, c33 =+4-10+6-3= -3. Μόνο δύο τιμές είναι αρνητικές οπότε διαλέγουμε την απολύτως μεγαλύτερη δηλ. αυτή που θα μειώσει περισσότερο το κόστος (c21 = -4).
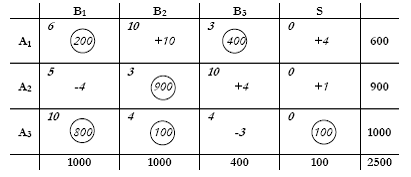
Για τη νέα λύση, δίνουμε στη Χ21 τη μικρότερη από τις γειτονικές τιμές στο βρόγχο υπολογισμού του c21 (γραμμή 1 ή στήλη 3) και ρυθμίζουμε ανάλογα τις υπόλοιπες β.μ. όπως φαίνεται στον παρακάτω πίνακα.
Το συνολικό κόστος της νέας λύσης είναι:
6·200+3·400+5·800+3·100+4·900+0·100 = 10300.
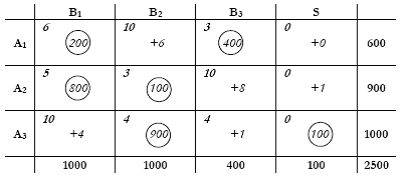
Βρίσκουμε ξανά για όλες τις μη β.μ. την οριακή επίδραση τους στο κόστος αν αυξηθούν κατά 1 μονάδα, αλλα όπως βλέπουμε στον πίνακα είναι όλες θετικές. Επομένως η λύση αυτή είναι η βέλτιστη.
Η τιμή της περιθωριακής μεταβλητής Χ34 = 100 μας πληροφορεί ότι αν εφαρμόσουμε αυτή τη λύση στο πρόβλημα μεταφοράς μπορούμε επίσης, αν θέλουμε, να μειώσουμε τη παραγωγή στο εργοστάσιο A3 κατά 100 τόνους.

