Προβλήματα Μεταφοράς
Μια άλλη κατηγορία προβλημάτων, όπου είναι δυνατή η εφαρμογή της βελτιστοποίησης μέσω του Γραμμικού Προγραμματισμού, είναι τα προβλήματα των μεταφορών.
Ένα τυπικό πρόβλημα μεταφοράς στη δομική και μη βιομηχανία διατυπώνεται ως εξής:
Σε κάποιες τοποθεσίες Α1, Α2, Α3, …, Αm, παράγεται ένα προϊόν σε ορισμένη ποσότητα ανά τοποθεσία και χρονικό διάστημα. Το σύνολο του προϊόντος καταναλώνεται σε κάποιες άλλες τοποθεσίες Β1, Β2, Β3, …, Βn, και σε καθορισμένες ποσότητες ανά τοποθεσία. Το κόστος μεταφοράς του προϊόντος από κάθε τοποθεσία Αi σε κάθε μια τοποθεσία Βj είναι επίσης ορισμένο και ίσο με Cij. Το ζητούμενο του προβλήματος είναι να βρεθεί η ποσότητα του προϊόντος Xij που θα μεταφερθεί από κάθε Αi σε κάθε Βj ώστε το συνολικό κόστος των μεταφορών να είναι το ελάχιστο δυνατό.
Το πρόβλημα αυτό λόγω της ειδικής μορφής του, αν και μπορεί να λυθεί με τη μέθοδο Simplex, λύνεται με άλλες απλούστερες μεθόδους που βασίζονται στη ίδια τεχνική και αναπτύχθηκαν επίσης από τον Dantzig και άλλους όπως οι Charnes και Coopers.
Μοντελοποίηση του Κλασικού Προβλήματος Μεταφοράς
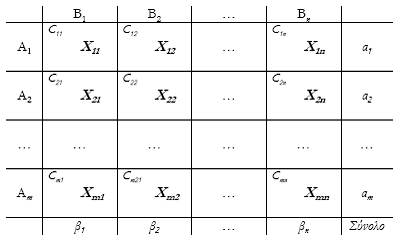
Για να σχεδιάσουμε το μοντέλο του προβλήματος θεωρούμε κατ’ αρχήν ότι, στα σημεία Α1, Α2, …, Αm, θα παράγονται αντίστοιχα α1, α2, …, αm, μονάδες προϊόντος, στα σημεία Β1, Β2, Β3, …, Βn, θα καταναλώνονται αντίστοιχα β1, β2, …, βn, μονάδες προϊόντος, και, Xij θα είναι οι μονάδες προϊόντος που θα μεταφερθούν από το σημείο παραγωγής Αi στο σημείο κατανάλωσης Βj, με κόστος μεταφοράς ανά μονάδα Cij αντίστοιχα.
Οι περιορισμοί του προβλήματος είναι οι παρακάτω:
Το σύνολο των αποστολών από κάθε σημείο Αi σε όλα τα σημεία Βj, θα είναι ίσο με αi.
- Το σύνολο των παραλαβών σε κάθε σημείο Βj από όλα τα σημεία Αi, θα είναι ίσο με βj.
- Η παραγωγή είναι ίση με τη κατανάλωση (αν υπάρχει έλλειψη ή περίσσεια χρησιμοποιούμε μεταβλητές περιθωρίου S όπως θα δούμε αργότερα).
- Οι ποσότητες Xij είναι θετικές ή μηδέν ( Xij ≥ 0, i= 1,..,m, j= 1,..,n).
Η Α.Σ. του προβλήματος είναι η ελαχιστοποίηση του κόστους μεταφοράς το οποίο υπολογίζεται από το κόστος όλων των διαδρομών Cij·Xij :
Για να λύσουμε το πρόβλημα τοποθετούμε τα πιο πάνω δεδομένα όπως φαίνεται στον επόμενο πίνακα επίλυσης, ώστε στη συνέχεια να εφαρμόσουμε μια παραλλαγή της μεθόδου Simplex, που έχει σχεδιαστεί για αυτή τη κατηγορία προβλημάτων.