Επίλυση πιο Σύνθετων Προβλημάτων Γραμμικού Προγραμματισμού
Τα πραγματικά ΠΓΠ είναι συνήθως πολύ πιο σύνθετα με πολλές παραμέτρους, πολλές μεταβλητές και με πολλούς και αντικρουόμενους περιορισμούς. Παρακάτω θα δούμε σταδιακά μερικές πιο σύνθετες μορφές.
ΠΡΟΒΛΗΜΑ 3
Ένας αγρότης μπορεί να χρησιμοποιήσει δυο τύπους λιπασμάτων Α και Β. Σε κάθε σακί ο τύπος Α περιέχει 10 μονάδες Φωσφόρου, 3 Καλίου και 6 Αζώτου, ενώ, σε κάθε σακί τύπου Β περιέχονται 12 μονάδες Φωσφόρου, 5 Καλίου και 7 Αζώτου. Στην έκταση που καλλιεργεί χρειάζεται: το πολύ 1200 μον. Φωσφόρου και τουλάχιστον 315 μον. Καλίου και 504 Αζώτου. Αν ο τύπος Α κοστίζει 16 € το σακί και ο Β 20 € το σακί, πόσα σακιά από το κάθε είδος πρέπει να προμηθευτεί για να έχει το ελάχιστο κόστος;
ΜΟΝΤΕΛΟΠΟΙΗΣΗ:
1. Μεταβλητές :
α) αριθμός σακιών τύπου Α: Χ,
β) αριθμός σακιών τύπου Β: Υ.
2. Παράμετροι :
α) ο τύπος Α κοστίζει 16 € και περιέχει: 10 Φω, 3 Κα, 6 Αζ,
β) ο τύπος Β κοστίζει 20 € και περιέχει: 12 Φω, 5 Κα, 7 Αζ,
3. Περιορισμοί :
Η έκταση χρειάζεται:
α) το πολύ 1200 Φω,
β) τουλάχιστον 315 Κα, και,
γ )τουλάχιστον 504 Αζ.
δ) εννοείται επίσης ότι: Χ, Υ ≥ 0.
4. Αντικειμενικός στόχος :
Το συνολικό κόστος από την αγορά των σακιών Α (X·16 €) και Β (Υ·20 €) θα πρέπει να γίνει όσο το δυνατόν μικρότερο (min).
5. Πίνακας :
Όταν έχουμε πολλούς περιορισμούς ή/και μεταβλητές, μας διευκολύνει να συγκεντρώσουμε σε ένα πίνακα όλα τα στοιχεία. Από τον πίνακα αυτόν προκύπτουν άμεσα οι ανισότητες του μοντέλου:
| Τύπος Α | Τύπος Β | Περιορισμοί | |
| Μεταβλητές (σακ) | Χ | Υ | |
| Φω (μον/σακ) | 10 | 12 | max 1200 (μον) |
| Κα (μον/σακ) | 3 | 5 | min 315 (μον) |
| Αζ (μον/σακ) | 6 | 7 | min 504 (μον) |
| Κόστος (€/σακ) | 16 | 20 | Ελάχιστο (min) |
Μοντέλο:
ΥΤΠ: Χ ≥ 0 & Υ ≥ 010Χ + 12Υ ≤ 1200
3Χ + 5Υ ≥ 315
6Χ + 7Υ ≥ 504
ΑΣ: min ( 16Χ + 20Υ ).
ΓΡΑΦΙΚΗ ΛΥΣΗ:
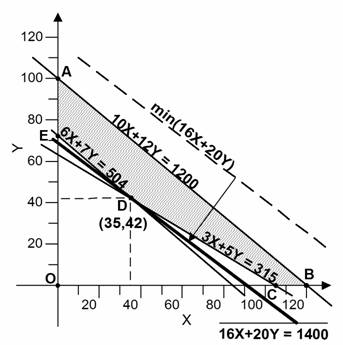
Η ΑΣ ελαχιστοποιείται στο σημείο D οπότε οι βέλτιστες τιμές των Χ & Υ είναι οι συντεταγμένες του, Χ = 35 και Υ = 42. Δηλαδή η πιο οικονομική επιλογή είναι 35 σακιά τύπου Α και 42 τύπου Β με συνολικό κόστος 1400.
ΑΛΓΕΒΡΙΚΗ ΛΥΣΗ (ΣΥΣΤΗΜΑ ΕΞΙΣΩΣΕΩΝ):
Η πρώτη βασική διαπίστωση από τη γραφική λύση είναι ότι οι βέλτιστες τιμές βρίσκονται πάντα σε κάποια κορυφή της εφικτής περιοχής. Οι κορυφές αυτές δεν είναι τίποτα άλλο από τη τομή δύο ευθειών που σχεδιάστηκαν από τις αντίστοιχες ανισότητες των περιορισμών.
Άρα, αντί να μελετάμε ολόκληρη τη περιοχή των (άπειρων) εφικτών λύσεων, αρκεί να βρούμε μόνο τις κορυφές της περιοχής. Αυτό γίνεται εύκολα λύνοντας τα πιθανά συστήματα που προκύπτουν παίρνοντας ανά δύο τις ‘εξισώσεις-περιορισμούς’.
Στο παράδειγμά μας οι συνδυασμοί των 5 ευθειών ανά 2 μας δίνουν το πλήθος των σημείων.
- 10Χ + 12Υ = 1200
- 3Χ + 5Υ = 315
- 6Χ + 7Υ = 504
- Χ = 0
- Υ = 0
Συνδυασμοί των 5 ανά 2 = ( 5! )/( 3! · 2!) = 10 σημεία.
Αν ξανασχεδιάσουμε το προηγούμενο διάγραμμα ώστε να φαίνονται όλα τα σημεία τομής των ευθειών, θα διαπιστώσουμε ότι δεν είναι όλα αποδεκτά.

Από αυτό το αριθμήσιμο πλήθος λύσεων θα πρέπει αποκλειστούν όσες δεν είναι εφικτές. Γι’ αυτό ελέγχουμε κάθε σημείο αν ικανοποιεί τους υπόλοιπους 3 περιορισμούς, και μόνο για όσα αποδειχθούν εφικτά υπολογίζουμε τη τιμή της ΑΣ. Φυσικά το σημείο που δίνει τη μεγαλύτερη ή μικρότερη (ανάλογα με το ζητούμενο) τιμή της ΑΣ θα είναι και η βέλτιστη λύση. Αυτή η υπολογιστική διαδικασία αν γραφεί μεθοδικά μας δίνει τον παρακάτω πίνακα:
Ζεύγη |
Λύση |
Εφικτό |
Τιμή |
| 1, 2 | I : (158.6, -32.1) | OXI | - |
| 1, 3 | H : (-1176, 1080) | OXI | - |
| 1, 4 | A : (0, 100) | NAI | 2000 |
| 1, 5 | B : (120, 0) | NAI | 1920 |
| 2, 3 | D : (35, 42) | NAI | 1400 |
| 2, 4 | G : (0, 63) | OXI | - |
| 2, 5 | C : (105, 0) | NAI | 1680 |
| 3, 4 | E : (0, 72) | NAI | 1440 |
| 3, 5 | F : (84, 0) | OXI | - |
| 4, 5 | O : (0, 0) | OXI | - |
Ο παραπάνω τρόπος λύσης, δηλαδή με το συνδυασμό των περιορισμών ανά δυο, μας λύνει οποιοδήποτε πρόβλημα ΓΠ, και όχι μόνο τα 2-D ΠΓΠ που λύνει η γραφική μέθοδος.
Ανάγκη Αποδοτικότερων Μεθόδων
Ένα πρόβλημα με 3 μεταβλητές θα μπορούσε ίσως να λυθεί γραφικά σε 3-D χώρο, όπου οι περιορισμοί είναι ολόκληρα επίπεδα και οι τομές τους ευθείες και μόνο οι τομές 3 επιπέδων θα είναι σημεία. Δεν είναι όμως κάτι απλό ούτε εύκολο.
Αν λοιπόν έχουμε ένα πρόβλημα με γενικά m περιορισμούς και n μεταβλητές τότε το πρόβλημά μας θα παρουσίαζε τα εξής χαρακτηριστικά:
- Ο χώρος του είναι n-διαστάσεων
- Κάθε κορυφή του θα είναι η τομή n υπερ-επιπέδων
- Για κάθε σημείο θα πρέπει να λυθεί ένα σύστημα n εξισώσεων με n αγνώστους
- Το πλήθος των σημείων και των συστημάτων γίνεται πολύ μεγάλος αριθμός για μεγάλα m και n(όλοι οι συνδυασμοί των m+n ανά n).
Τα παραπάνω φανερώνουν την ανάγκη να υπάρξει μια πιο αποδοτική μέθοδος για την βέλτιστη λύση των ΠΓΠ. Η μέθοδος αυτή υπάρχει, προτάθηκε από τον G. Dantzig το 1947, και λέγεται μέθοδος SIMPLEX.
Ανάλυση Ειδικών Μορφών Προβλημάτων ΓΠ
Πριν περάσουμε στη μέθοδο Simplex θα δούμε μερικές ειδικές περιπτώσεις που παρουσιάζονται στα ΠΓΠ και εξηγούνται καλύτερα με το γραφική μέθοδο.
ΑΠΕΡΙΟΡΙΣΤΗ ΛΥΣΗ
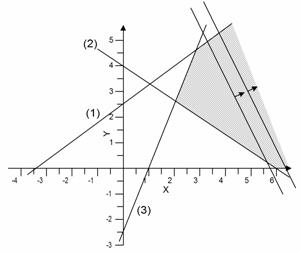
Αν σε ένα πρόβλημα μεγιστοποίησης η εφικτή περιοχή δεν είναι φραγμένη από τη «πάνω» μεριά, ή, αντίστοιχα σε ένα πρόβλημα ελαχιστοποίησης η εφικτή περιοχή δεν είναι φραγμένη από τη «κάτω» μεριά, τότε η λύση μας είναι μη πεπερασμένη. Στη περίπτωση αυτή η ΑΣ μπορεί να αυξάνει ή να μειώνεται απεριόριστα χωρίς ποτέ να φτάσει στα όρια της εφικτής περιοχής, και η βέλτιστη λύση τείνει στο άπειρο.
ΑΠΕΙΡΙΑ ΛΥΣΕΩΝ
Αν η ευθεία της ΑΣ τύχει να είναι παράλληλη με μια από τις ευθείες των περιορισμών, και φτάνοντας στην άκρη της εφικτής περιοχής συμπέσει με την ευθεία αυτή, τότε, η βέλτιστη λύση αντί να είναι ένα μόνο σημείο είναι ένα ολόκληρο ευθύγραμμο τμήμα. Σε αυτή τη περίπτωση, κάθε ένα από τα άπειρα σημεία του ευθύγραμμου τμήματος είναι και μια βέλτιστη λύση του ΠΓΠ, δηλαδή έχουμε άπειρες βέλτιστες λύσεις. Όλες αυτές οι λύσεις είναι ισοδύναμες και δίνουν την ίδια τιμή στην ΑΣ.
ΑΔΥΝΑΤΗ ΛΥΣΗ
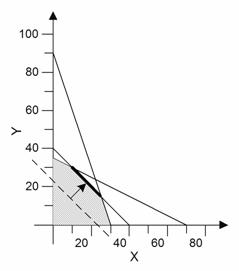
Υπάρχουν φυσικά προβλήματα όπου οι περιορισμοί δεν ορίζουν καμία εφικτή περιοχή στην οποία, δηλαδή, όλες μαζί οι συνθήκες να ικανοποιούνται. Τότε δεν είναι δυνατόν να υπάρξουν εφικτές λύσεις, πόσο μάλλον βέλτιστες λύσεις. Το σύστημα των περιορισμών είναι επομένως ασυμβίβαστο και η λύση του ΠΓΠ είναι αδύνατη.
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΙΔΙΚΩΝ ΜΟΡΦΩΝ
Απεριόριστη Λύση: ΥΤΠ: ΑΣ: |
|
Απειρία Λύσεων: ΥΤΠ: ΑΣ: |
|
Αδύνατη Λύση: ΥΤΠ: ΑΣ: |
|