Η Μέθοδος SIMPLEX
Η μέθοδος αυτή προτάθηκε από τον G. Dantzig το 1947, εφαρμόζεται ακόμη και σε προβλήματα που έχουν χιλιάδες μεταβλητές και περιορισμούς.και είναι ιδανική για επίλυση μέσω Η/Υ.
Βασικές Έννοιες της Μεθόδου Simplex
Στα επόμενα βήματα θα χρησιμοποιηθεί το διδιάστατο ΠΓΠ που λύσαμε με τη γραφική μέθοδο στο Παράδειγμα 2, ώστε να είναι πιο εύκολη η σχεδίαση, σύγκριση και η αντιστοίχιση των λύσεων. Για τη γενικότητα της μεθόδου, δεν χρησιμοποιούνται τα Χ & Υ στις μεταβλητές, αλλά τα Χ1, Χ2, Χ3, κλπ.
ΤΥΠΟΠΟΙΗΜΕΝΗ ΜΟΡΦΗ ΤΟΥ ΜΟΝΤΕΛΟΥ
Για να μπορέσουμε να εφαρμόσουμε τη μέθοδο, το μοντέλο μας πρέπει να είναι σε τυποποιημένη μορφή. Η τυποποιημένη μορφή (standard form) ενός προβλήματος μεγιστοποίησης είναι η μορφή στην οποία οι ανισότητες (περιορισμοί) είναι όλες ≤ και το δεξί μέλος τους είναι θετικός αριθμός.
Το μοντέλο από το Παράδειγμα 2, είναι ήδη σε τυποποιημένη μορφή:
ΑΣ: Μέγιστο Ρ = 60·Χ1 + 40·Χ2 (κέρδος)
ΥΤΠ:
1) Χ1 + Χ2 ≤ 50 (περιορισμός αποθήκης)
2) 40·Χ1 + 20·Χ2 ≤ 1400 (περιορισμός χρημάτων)
3) Χ1, Χ2 ≥ 0 (μη αρνητικές μεταβλητές)
ΜΕΤΑΒΛΗΤΕΣ ΠΕΡΙΘΩΡΙΟΥ
Όπως έγινε και στην αλγεβρική λύση που είδαμε νωρίτερα, οι διαδικασίες που θα χρησιμοποιήσει η μέθοδος Simplex απαιτούν τη γραφή των περιορισμών με τη μορφή εξισώσεων αντί των ανισοτήτων.
Στις ανισότητες των περιορισμών, το αριστερό μέλος είναι μικρότερο ή ίσο του δεξιού μέλους. Για να γίνουν οι περιορισμοί ισότητες, πρέπει να τους προσθέσουμε κάτι στο πρώτο μέλος που θα εξαλείψει τη διαφορά. Προσθέτουμε λοιπόν στο αριστερό μέλος των περιορισμών 1 & 2, από μία βοηθητική μεταβλητή, τις S1 & S2 αντίστοιχα, και έχουμε:
1) Χ1 + Χ2 + S1 = 50
2) 40·Χ1 + 20·Χ2 + S2 = 1400
Για να καταλάβουμε το φυσικό ρόλο των νέων μεταβλητών, αρκεί να κοιτάξουμε τη γραφική επίλυση του προβλήματος και να εφαρμόσουμε τα αποτελέσματα (Χ1 = 20, Χ2 =30). Τότε θα δούμε ότι η μεταβλητή S1 μας δίνει το διαθέσιμο χώρο στην αποθήκη, και η μεταβλητή S2 μας δίνει τα διαθέσιμα χρήματα. Όταν λοιπόν βρεθεί η λύση ενός ΠΓΠ, οι βοηθητικές μεταβλητές (S1, S2, κλπ.) περιέχουν τα αποθέματα που θα μας έχουν περισσέψει σε: χώρο, χρήμα, χρόνο, πρώτες ύλες, και σε ό,τι άλλο περιορισμό είχαμε βάλει. Για να τις διακρίνουμε από τις κανονικές μεταβλητές (Χ1, Χ2, κλπ.), στη συνέχεια θα αποκαλούμε τις νέες μεταβλητές (S1, S2, κλπ.), μεταβλητές περιθωρίου (slack variables), καθώς αντιπροσωπεύουν το περιθώριο (slack) μεταξύ της λύσης μας και των ορίων του περιορισμού.
ΒΑΣΙΚΕΣ & ΒΑΣΙΚΕΣ ΕΦΙΚΤΕΣ ΛΥΣΕΙΣ
Το σύστημα των περιορισμών 1 & 2 που προκύπτει, έχει 2 εξισώσεις και 4 μεταβλητές και προφανώς μια απειρία λύσεων. Όπως όμως είδαμε στα προηγούμενα κεφάλαια, η βέλτιστη λύση βρίσκεται σε τομή των ευθειών κάποιων περιορισμών. Με το σκεπτικό αυτό, νωρίτερα στην αλγεβρική μέθοδο, λύσαμε όλα τα πιθανά συστήματα εξισώσεων, βρήκαμε όλα τα σημεία τομής των ευθειών των περιορισμών, και τέλος επιλέξαμε, τη βέλτιστη λύση. Παρόμοιο αλλά πιο σύντομο δρόμο ακολουθεί η μέθοδος Simplex.
Οι λύσεις των ΠΓΠ διακρίνονται σε δυο κατηγορίες. Όσες βρίσκονται στα σημεία τομής των ορίων των περιορισμών, λέγονται βασικές λύσεις. Όσες από τις βασικές λύσεις αποτελούν και άκρα (κορυφές) της εφικτής περιοχής λέγονται βασικές εφικτές λύσεις.
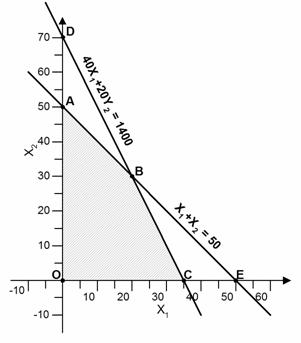
Εφικτή Περιοχή (OABC), Βασικές Λύσεις (A,B,C,D,E,O), και,
Βασικές Εφικτές Λύσεις (A,B,C,O).
ΒΑΣΙΚΕΣ & ΜΗ-ΒΑΣΙΚΕΣ ΜΕΤΑΒΛΗΤΕΣ
Για να βρεθούν οι βασικές λύσεις θα πρέπει να εφαρμόσουμε κάτι παρόμοιο με την αλγεβρική μέθοδο, που να μην έχει όμως τα ελαττώματά της.
Οι μεταβλητές μας (κανονικές και περιθωρίου) είναι περισσότερες από τις εξισώσεις. Τις χωρίζουμε λοιπόν αυθαίρετα σε δύο ομάδες, μία που να έχει τόσες μεταβλητές όσες είναι και οι εξισώσεις, και μία με όλες τις υπόλοιπες. Τη πρώτη ομάδα την ονομάζουμε βασικές μεταβλητές και τη δεύτερη μη-βασικές μεταβλητές.
Αφού οι βασικές μεταβλητές είναι όσες και οι εξισώσεις, θέτοντας όλες τις άλλες μη-βασικές μεταβλητές ίσες με το 0, μπορούμε να λύσουμε το σύστημα. Η λύση που θα βρούμε είναι μια βασική λύση του προβλήματος. Για παράδειγμα, μπορούμε να θέσουμε όλες τις κανονικές μεταβλητές ίσες με 0 και να λύσουμε για τις μεταβλητές περιθωρίου που είναι όσες και οι εξισώσεις. Αυτή η λύση αν και τετριμμένη είναι και πιο συνηθισμένη αρχική επιλογή.
Παράδειγμα:
1η Βασική Λύση. (S1, S2: Βασικές, Χ1 = Χ2 = 0: Μη-Βασικές)
Χ1 + Χ2 + S1 = 50 => S1 = 50
40·Χ1 + 20·Χ2 + S2 = 1400 => S2 = 1400
2η Βασική Λύση. (S1, X2: Βασικές, Χ1 = S2 = 0: Μη-Βασικές)
Χ1 + Χ2 + S1 = 50 => S1 = 50-70 = -20
40·Χ1 + 20·Χ2 + S2 = 1400 => X2 = 1400/20 =70
3η ...κλπ. ...
Αν στο σημείο αυτό συνεχίζαμε και πραγματοποιούσαμε όλους τους δυνατούς συνδυασμούς επιλογής μεταβλητών, θα είχαμε σχεδόν επαναλάβει την αλγεβρική μέθοδο και θα είχαμε βρει όλες τις βασικές λύσεις, εφικτές και μη. Οι συνδυασμοί και οι λύσεις θα μπορούσαν να τοποθετηθούν σε ένα πίνακα όπως στην αλγεβρική μέθοδο:
| Βασικές Λύσεις | Συντεταγμ. σημείου |
Τομή των ευθειών περιορισμών |
Εφικτή λύση |
|||
| Χ1 | Χ2 | S1 | S2 | |||
| 0 | 0 | 50 | 1400 | Ο(0, 0) | Χ1 = 0 Χ2 = 0 |
Ναι |
| 0 | 70 | -20 | 0 | D(0, 70) | Χ1 = 0 40·Χ1+20·Χ2=1400 |
Όχι |
| ... κ.λ.π. ... | ||||||
Όμως, θα πρέπει η μέθοδος μας να αποφεύγει να λύνει όλους τους πιθανούς συνδυασμούς συστημάτων, οι οποίοι μπορεί να ανέρχονται και σε εκατοντάδες.
Παρατηρώντας τις βασικές λύσεις του ΠΓΠ προκύπτει επίσης ότι:
Α) Οι βασικές εφικτές λύσεις συνδέονται με τις κορυφές τις εφικτής περιοχής, μία από τις οποίες είναι και η βέλτιστη λύση του ΠΓΠ, και,
Β) Οι μη-εφικτές λύσεις έχουν τουλάχιστον μια αρνητική τιμή, ενώ οι εφικτές δεν έχουν καμία αρνητική τιμή.
Τα Βήματα της Μεθόδου Simplex
Ο ΠΙΝΑΚΑΣ SIMPLEX
Στα επόμενα βήματα της μεθόδου θα πρέπει να εντοπίσουμε τη βέλτιστη λύση χωρίς να πρέπει να υπολογίσουμε κάθε γωνία της εφικτής περιοχής. Η σημασία της γίνεται μεγαλύτερη όσο αυξάνουν οι μεταβλητές και οι περιορισμοί όποτε φτάνουμε σε εφικτές περιοχές με δεκάδες και εκατοντάδες γωνιών. Τα δυο πρώτα στάδια αφορούν τη δημιουργία του Πίνακα Simplex.
- Στο σύστημα των περιορισμών προσθέτουμε και την εξίσωση της μεγιστοποίησης (Α.Σ.) και δημιουργούμε το καλούμενο Αρχικό Σύστημα της μεθόδου Simplex:
1) Χ1 + Χ2 + S1 = 50
2) 40·Χ1 + 20·Χ2 + S2 = 1400
3) -60·Χ1 - 40·Χ2 + P = 0
Στο σύστημα αυτό η P θα είναι πάντα μία από τις βασικές μεταβλητές. Κάθε βασική λύση του συστήματος είναι και βασική λύση του ΠΓΠ αφού αφαιρεθεί η P. Επίσης, η P είναι η μόνη που επιτρέπεται να πάρει αρνητική τιμή στις βασικές εφικτές λύσεις, μια και δεν είναι κανονική μεταβλητή.
- Αρχίζουμε τη μέθοδο με μια βασική εφικτή λύση την οποία καλούμε αρχική βασική εφικτή λύση. Η λύση αυτή βρίσκεται εύκολα και συνδέεται με την αρχή των αξόνων. Είναι η τετριμμένη λύση όπου όλες οι κανονικές μεταβλητές είναι μηδέν (επιλέγονται σαν μη-βασικές) και σαν βασικές μεταβλητές (β.μ.) επιλέγονται οι μεταβλητές περιθωρίου S και η P (που είναι όσες και οι εξισώσεις). Όπως είδαμε και νωρίτερα η βασική αυτή λύση δίνει:
Χ1 = 0, Χ2 = 0, S1 = 50, S2 = 1400, και P = 0
η οποία είναι βασική και εφικτή αφού όλα τα Χ και S είναι μη-αρνητικά. Η λύση αν και οριακή είναι εφικτή και έχει φυσικό νόημα αφού, αν δεν αγοραστεί κανένα προϊόν (Χ1 = 0, Χ2 = 0), το κέρδος είναι μηδέν (P = 0), η αποθήκη άδεια (S1 = 50) και τα χρήματα αξόδευτα (S2 = 1400).
Για να διευκολύνουμε τους υπολογισμούς της μεθόδου τοποθετούμε το αρχικό σύστημα των τριών εξισώσεων σε μορφή πίνακα ο οποίος λέγεται Αρχικός Πίνακας Simplex.
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | |
| S1 | 1 | 1 | 1 | 0 | 0 | 50 |
| S2 | 40 | 20 | 0 | 1 | 0 | 1400 |
| P | -60 | -40 | 0 | 0 | 1 | 0 |
Ο αρχικός πίνακας Simplex περιέχει την αρχική βασική εφικτή λύση που είδαμε πιο πάνω. Για (Χ1 = 0, Χ2 = 0) οι τιμές των βασικών μεταβλητών (β.μ.) δίνονται από τη τελευταία στήλη.
OΙ ΕΠΑΝΑΛΗΨΕΙΣ ΤΗΣ SIMPLEX
Το τρίτο στάδιο περιέχει 1, 2, ή, περισσότερα επαναληπτικά βήματα όπου πρέπει να βρίσκουμε όλο και καλύτερες βασικές εφικτές λύσεις έως ότου φτάσουμε στη βέλτιστη.
- Σε κάθε επανάληψη η μέθοδος Simplex αντικαθιστά μια βασική μεταβλητή από μια μη-βασική.
Η επιλογή της μη-βασικής (εισερχόμενης) και της βασικής (εξερχόμενης) γίνεται ως εξής:
Α) Πρώτα επιλέγεται η μη-βασική μεταβλητή που θα αυξήσει περισσότερο την ΑΣ (κέρδος). Είναι αυτή που έχει το μεγαλύτερο συντελεστή στον υπολογισμό του P (ή μικρότερο αρνητικό στον πίνακα). Στη περίπτωσή μας είναι η Χ1 που έχει συντελεστή 60 για το Ρ (ή -60 στον πίνακα). Η στήλη της εισερχόμενης μεταβλητής ονομάζεται οδηγός (pivot) στήλη.
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | |
| S1 | 1 | 1 | 1 | 0 | 0 | 50 |
| S2 | 40 | 20 | 0 | 1 | 0 | 1400 |
| P | -60 | -40 | 0 | 0 | 1 | 0 |
Β) Μετά επιλέγεται η βασική μεταβλητή που περιορίζει περισσότερο τη μη-βασική μεταβλητή που διαλέξαμε. Αυτή βρίσκεται διαιρώντας τη τελευταία στήλη δια την οδηγό στήλη και επιλέγοντας το μικρότερο αποτέλεσμα. Στη περίπτωσή μας είναι η S2 που δίνει αποτέλεσμα 35 (<50). Η γραμμή της εξερχόμενης μεταβλητής ονομάζεται οδηγός (pivot) γραμμή. Το στοιχείο του πίνακα στο οποίο διασταυρώνει η οδηγός γραμμή την οδηγό στήλη λέγεται οδηγό (pivot) στοιχείο.
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | ||
| S1 | 1 | 1 | 1 | 0 | 0 | 50 | 50/1 = 50 |
| S2 | 40 | 20 | 0 | 1 | 0 | 1400 | 1400/40 = 35 |
| P | -60 | -40 | 0 | 0 | 1 | 0 |
Η αντικατάσταση της εξερχόμενης S2 από την εισερχόμενη (στις β.μ.) Χ1 γίνεται ως εξής:
Α) Διαιρούμε ολόκληρη την οδηγό γραμμή με το οδηγό στοιχείο, ώστε αυτό να γίνει 1 (αν είναι ήδη 1, το βήμα αυτό παραλείπεται),
| 40 | 20 | 0 | 1 | 0 | 1400 |
| 1 | ½ | 0 | 1/40 | 0 | 35 |
και ο πίνακας Simplex γίνεται:
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | |
| S1 | 1 | 1 | 1 | 0 | 0 | 50 |
| S2 | 1 | ½ | 0 | 1/40 | 0 | 35 |
| P | -60 | -40 | 0 | 0 | 1 | 0 |
Β) Προσθαφαιρούμε, ανάλογα, την οδηγό γραμμή στις υπόλοιπες γραμμές, όσες φορές χρειάζεται, για να γίνουν μηδέν τα υπόλοιπα στοιχεία της οδηγού στήλης,
| 1 | 1 | 1 | 0 | 0 | 50 |
| 1 | ½ | 0 | 1/40 | 0 | 35 |
| 0 | ½ | 1 | -1/40 | 0 | 15 |
και,
| -60 | -40 | 0 | 0 | 1 | 0 |
| 1 | ½ | 0 | 1/40 | 0 | 35 |
| 0 | -10 | 0 | 60/40 | 1 | 2100 |
και ο πίνακας Simplex γίνεται:
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | |
| S1 | 0 | ½ | 1 | -1/40 | 0 | 15 |
| Χ1 | 1 | ½ | 0 | 1/40 | 0 | 35 |
| P | 0 | -10 | 0 | 60/40 | 1 | 2100 |
Γ) Τοποθετούμε τη μεταβλητή Χ1 στις βασικές μεταβλητές και βλέπουμε το αποτέλεσμα στη τελευταία στήλη. Η λύση που παίρνουμε είναι Χ1 = 35, Χ2 = 0, και δίνει κέρδος P = 2100, που είναι σαφώς καλύτερο από το 0 της αρχικής λύσης.
Η λύση μπορεί να βελτιωθεί κι’ άλλο. Αυτό φαίνεται από τη παρουσία αρνητικών αριθμών (-10) στη γραμμή του P.
- Η διαδικασία (3) επαναλαμβάνεται με τον ίδιο ακριβώς τρόπο όσες φορές χρειαστεί έως ότου βρεθεί η βέλτιστη λύση (δηλ. δεν υπάρχουν αρνητικοί αριθμοί στη γραμμή του Ρ):
Στο βήμα αυτό επιλέγεται σαν εισερχόμενη (να μπει στις β.μ.) η μεταβλητή Χ2 που αυξάνει το P περισσότερο (-10), και, σαν εξερχόμενη (που θα αντικατασταθεί) η S1 που περιορίζει την Χ2 περισσότερο (15/ ½ =30 <70).
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | ||
| S1 | 0 | ½ | 1 | -1/40 | 0 | 15 | 15 / ½ = 30 |
| Χ1 | 1 | ½ | 0 | 1/40 | 0 | 35 | 35 / ½ = 70 |
| P | 0 | -10 | 0 | 60/40 | 1 | 2100 |
Επαναλαμβάνουμε τη διαδικασία αντικατάστασης της S1 από την Χ2.
Α) Κάνουμε 1 το οδηγό στοιχείο διαιρώντας όλη την οδηγό γραμμή με αυτό,
| 0 | ½ | 1 | -1/40 | 0 | 15 |
| 0 | 1 | 2 | -2/40 | 0 | 30 |
και ο πίνακας Simplex γίνεται:
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | |
| S1 | 0 | 1 | 2 | -2/40 | 0 | 30 |
| Χ1 | 1 | ½ | 0 | 1/40 | 0 | 35 |
| P | 0 | -10 | 0 | 60/40 | 1 | 2100 |
Β) Κάνουμε 0 τα υπόλοιπα στοιχεία της στήλης προσθαφαιρώντας ανάλογα την οδηγό γραμμή.
| 1 | ½ | 0 | 1/40 | 0 | 35 |
| 0 | 1 | 2 | -2/40 | 0 | 30 |
| 1 | 0 | -1 | 2/40 | 0 | 20 |
και,
| 0 | -10 | 0 | 60/40 | 1 | 2100 |
| 0 | 1 | 2 | -2/40 | 0 | 30 |
| 0 | 0 | 20 | 2 | 1 | 2400 |
και ο πίνακας Simplex γίνεται:
| β.μ. | Χ1 | Χ2 | S1 | S2 | P | |
| Χ2 | 0 | 1 | 2 | -2/40 | 0 | 30 |
| Χ1 | 1 | 0 | -1 | 2/40 | 0 | 20 |
| P | 0 | 0 | 20 | 2 | 1 | 2400 |
Γ) Τοποθετούμε τη μεταβλητή Χ2 στις βασικές μεταβλητές και διαβάζουμε τη λύση στη τελευταία στήλη. Η λύση που παίρνουμε είναι Χ1 = 20, Χ2 = 30, και δίνει κέρδος P = 2400, που είναι καλύτερο από το 2100 της προηγούμενης λύσης.
Η λύση δεν μπορεί να βελτιωθεί κι’ άλλο. Αυτό φαίνεται και από τη απουσία αρνητικών αριθμών στη γραμμή του P. Κατά συνέπεια έχουμε βρει τη βέλτιστη λύση του προβλήματος.
Η λύση είναι η ίδια με τη λύση του ίδιου ΠΓΠ με τη γραφική μέθοδο που είδαμε σε προηγούμενο κεφάλαιο. Μάλιστα τα βήματα της μεθόδου Simplex φαίνονται στο παραάτω διάγραμμα με τις βασικές και εφικτές λύσεις του ΠΓΠ και είναι με τη σειρά τα σημεία: O, C & B.