Εφαρμογές Βελτιστοποίησης και Επιχειρησιακής Έρευνας σε Προβλήματα Μηχανικών

Γραμμικές Ανισότητες

Όπως είδαμε, τα παραπάνω προβλήματα μοντελοποιούνται σαν ένα σύνολο ανισοτήτων ή εξισώσεων. Ο πιο εύκολος τρόπος επίλυσής τους είναι μέσω της γραφικής μεθόδου. Η εφαρμογή της γραφικής μεθόδου είναι δυνατή όταν ένα πρόβλημα έχει δυο μεταβλητές, οπότε το μοντέλο του απεικονίζεται εύκολα σε ένα δισδιάστατο σύστημα αξόνων Χ και Υ. Σε ένα τέτοιο σύστημα αξόνων, μια γραμμική εξίσωση των Χ και Υ, απεικονίζεται σαν μια ευθεία και μια γραμμική ανισότητα αναπαρίσταται σαν ένα ημιεπίπεδο  που αρχίζει από την ευθεία της αντίστοιχης ισότητας.

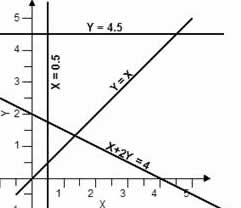
Παραδείγματα γραφικής απεικόνισης γραμμικών εξισώσεων & ανισοτήτων:

α) Υ = 4.5,      β) Χ = 0.5,       γ) Υ = Χ,        δ) Χ+2·Υ = 4,       ε) 4·Χ–Υ ≥ 0,      ζ) Χ+Υ ≥ 5.

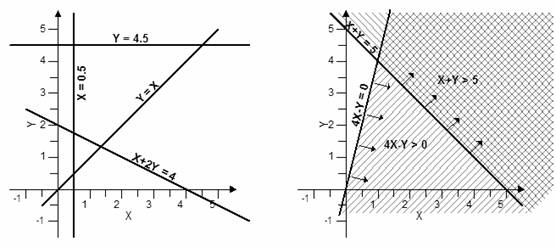
Με τη γραφική απεικόνιση μπορούμε εύκολα να εντοπίσουμε το σύνολο των εφικτών λύσεων και στη συνέχεια να βρούμε τη βέλτιστη λύση. Η μέθοδος αυτή λέγεται γραφική επίλυση προβλημάτων γραμμικού προγραμματισμού.

 

Γραφική Επίλυση των Προβλημάτων Γραμμικού Προγραμματισμού (ΠΓΠ)

Η γραφική επίλυση των ΠΓΠ ακολουθεί τα παρακάτω βήματα:

1. Σχεδιάζουμε ένα σύστημα αξόνων για τις μεταβλητές Χ και Υ.
2. Στη συνέχεια σχεδιάζουμε μια-μια κάθε ανισότητα του μοντέλου (δηλ. σχεδιάζουμε την αντίστοιχη ισότητα και αποκλείουμε το ημιεπίπεδο που δεν ικανοποιεί την ανισότητα).
3. Η περιοχή που απομένει περιέχει το σύνολο των εφικτών λύσεων, δηλαδή όσων δεν παραβιάζουν τους περιορισμούς ή τις συνθήκες.
4. Σχεδιάζουμε την αντικειμενική συνάρτηση και βρίσκουμε ποια από τις εφικτές λύσεις την μεγιστοποιεί ή την ελαχιστοποιεί (ανάλογα).
5. Οι συντεταγμένες του σημείου αυτού είναι οι βέλτιστες τιμές των Χ και Υ που ζητάμε.

ΕΠΙΛΥΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ 1

Το μοντέλο του προβλήματος είναι:

Υπό τους περιορισμούς (ΥΤΠ):
        Χ + Υ ≥ 12
        Χ + 2·Υ ≤ 16
        Χ ≥ 0, και, Υ ≥ 0.
ΑΣ:
        Να Βρεθούν Όλες οι Εφικτές Λύσεις

Σχεδιάζουμε τις παρακάτω ανισότητες (ημιεπίπεδα) και βρίσκουμε τη κοινή τους περιοχή:
        α)  Χ + Υ ≥ 12,     β)  Χ + 2·Υ ≤ 16,      γ)  Χ ≥ 0, και, Υ ≥ 0

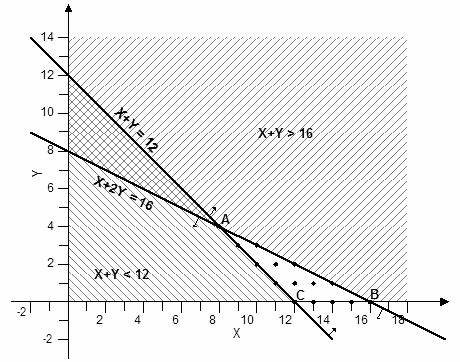
Η περιοχή ABC περιέχει όλες τις αποδεκτές λύσεις και συγκεκριμένα είναι όσα σημεία έχουν ακέραιες συντεταγμένες. Οι λύσεις αυτές αποτελούν το σύνολο των εφικτών λύσεων του προβλήματος.

Αν το πρόβλημα είχε και έναν αντικειμενικό στόχο τότε θα επιλέγαμε σαν βέλτιστη λύση το σημείο που θα τον ικανοποιούσε. Αν π.χ. μας ζητούσε να μεγιστοποιηθεί ο αριθμός των έγχρωμων καρτών, max(Υ), η βέλτιστη λύση θα ήταν το σημείο Α (Χ=8, Υ=4), ενώ αν ζητούσε το μέγιστο αριθμό αποδεκτών, max(Χ+Υ), θα ήταν το σημείο Β (Χ=16, Υ=0).

ΕΠΙΛΥΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ 2

Το μοντέλο του προβλήματος είναι:

Υπό τους περιορισμούς (ΥΤΠ):
        Χ + Υ ≤ 50
        2·Χ + Υ ≤ 70
        Χ ≥ 0, και, Υ ≥ 0.
ΑΣ:
        Να Μεγιστοποιηθεί το Συνολικό Κέρδος  60·Χ + 40·Υ,

Σχεδιάζουμε τις παρακάτω ανισότητες (ημιεπίπεδα) και βρίσκουμε τη κοινή τους περιοχή:
        α)  Χ + Υ ≤ 50,     β)  2·Χ + Υ ≤ 70,     γ)  Χ ≥ 0, και, Υ ≥ 0

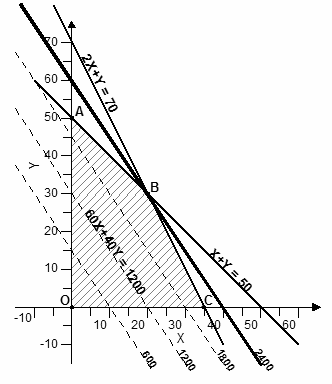
Η περιοχή ABCO μας δίνει τις εφικτές λύσεις του προβλήματος. Κάποια από αυτές θα είναι η καλύτερη λύση δηλαδή η βέλτιστη.

Για να τη βρούμε σχεδιάζουμε την αντικειμενική συνάρτηση (ΑΣ) για κάποιες τιμές κέρδους π.χ.: 
        60·Χ + 40·Υ = 600,   60·Χ + 40·Υ = 1200,   60·Χ + 40·Υ = 1800, κλπ.
Παρατηρούμε ότι όσο το συνολικό κέρδος αυξάνει, η ευθεία της ΑΣ απομακρύνεται από την αρχή των αξόνων. Όταν η ΑΣ φτάσει στο σημείο Β παίρνει τη μέγιστη δυνατή τιμή.

Οι συντεταγμένες του σημείου Β είναι επομένως οι βέλτιστες τιμές που ζητάμε, δηλαδή είναι: Χ = 20 και Υ = 30. Δίνοντας τις τιμές αυτές στην ΑΣ βρίσκουμε ότι το μέγιστο συνολικό κέρδος θα είναι 2400 €.

Ασκήσεις

1. Να λυθεί γραφικά το ΠΓΠ:

ΥΤΠ:      Χ, Υ ≥ 0
Χ + 2·Υ ≤ 8
2·Χ + Υ ≤ 10
ΑΣ:         max (5·Χ+5·Υ)

2. Να λυθεί γραφικά το ΠΓΠ:

ΥΤΠ:      Χ, Υ ≥ 0
3·Χ + 4·Υ ≥ 24
4·Χ + 3·Υ ≥ 24
ΑΣ:         min (8·Χ+7·Υ)

3. Να λυθεί γραφικά το ΠΓΠ:

ΥΤΠ:      Χ, Υ ≥ 0
Χ ≤ 6
2·Υ ≤ 10
3·Χ/2 + Υ ≤ 9
ΑΣ:         max (3·Χ + 5·Υ)

4. Να λυθεί γραφικά το ΠΓΠ:

ΥΤΠ:      Χ, Υ ≥ 0
20·Χ + 10·Υ ≤ 3000
Χ + Υ ≤ 200
ΑΣ:         max (1200·Χ + 900·Υ)

<<Προηγ. | ΤΜΗΜΑ | Επόμ.>>

------

Σημείωση: Ο Δικτυακός Τόπος είναι υπό κατασκευή και συνεχή επέκταση και βελτίωση. Η αρχική του μορφή αναπτύχθηκε στα πλαίσια του προγράμματος ΕΠΕΑΕΚ ΙΙ - "Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών" του Τμήματος Πολιτικών Έργων Υποδομής του ΤΕΙ Αθήνας.