Παράδειγμα: Το Πρόβλημα Κατανομής της Εταιρείας «Δομικές Μηχανές ΑΕ»
Η εταιρεία έχει αγοράσει 3 νέες δομικές μηχανές, ένα φορτωτή, ένα γαιοπροωθητή (bulldozer) και ένα γαιοδιαμορφωτή (grader). Οι μηχανές αυτές πρόκειται να εργαστούν για τους επόμενους μήνες συνεχώς σε διπλή 8ωρη βάρδια, και γι΄ αυτό χρειάζονται δυο χειριστές σε κάθε μηχανή.
Από τους υποψήφιους χειριστές που εξέτασε επιτροπή της εταιρείας έχουν επιλεγεί 6 χειριστές που είχαν τα περισσότερα προσόντα. Η επιτροπή βαθμολόγησε όλους τους χειριστές ως προς τις ικανότητές τους σε κάθε μηχανή, με κλίμακα 0 έως 10 (βαθμολογία 0 δίνεται σε περίπτωση που ο υποψήφιος αδυνατεί να εργαστεί σε μια μηχανή).
Ο πίνακας που ακολουθεί περιέχει τη βαθμολογία (Dij) των υποψηφίων (Β1, Β2, Β3, Β4, Β5, Β6) ανάλογα με την απόδοσή τους σε κάθε μια μηχανή (Α1, Α2, Α3)
| Β1 | Β2 | Β3 | Β4 | Β5 | Β6 | |
| Α1 | 10 | 7 | 7 | 10 | 5 | 8 |
| Α2 | 8 | 8 | 6 | 9 | 6 | 5 |
| Α3 | 9 | 7 | 8 | 8 | 0 | 0 |
Σκοπός μας είναι να ορίσουμε τα ζεύγη των χειριστών με βέλτιστο τρόπο ώστε να αυξηθεί η συνολική απόδοση των τριών μηχανημάτων.
ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΚΑΤΑΝΟΜΗΣ ΧΕΙΡΙΣΤΩΝ ΣΕ ΔΟΜΙΚΕΣ ΜΗΧΑΝΕΣ
Σχηματίζουμε τον πίνακα (όπως και στα προβλήματα μεταφοράς) και τοποθετούμε τα (Αi, Βj, & Dij). Στη θέση των μηδενικών (0) τοποθετούμε ένα μεγάλο αρνητικό αριθμό (-Μ).
Στη τελευταία στήλη βάζουμε τα αi = 2 (2 χειριστές σε κάθε μηχανή). Στη τελευταία γραμμή βάζουμε τα βj = 1 (1 μηχανή ανά χειριστή). Ο πίνακας θα έχει τη παρακάτω μορφή.
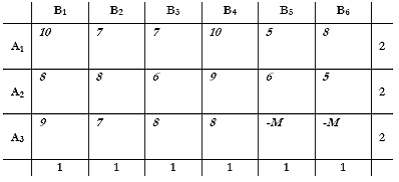
Επίλυση του Προβλήματος
Χρησιμοποιούμε τις ίδιες μεθόδους με τα προβλήματα μεταφοράς, μόνο που τώρα ενδιαφερόμαστε για τις μέγιστες ποσότητες.
ΑΡΧΙΚΗ ΛΥΣΗ – ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΟΥ ΠΙΝΑΚΑ
Με τη μέθοδο του ελάχιστου πίνακα βρίσκουμε μια αρχική βασική λύση με τη παρακάτω σειρά (αρχίζοντας από το μεγαλύτερο Dij ):
D11 = 10, Χ22 = min{2,1} = 1, & διαγράφονται τα: Χ21, Χ31.
D14 = 10, Χ14 = min{2-1,1} = 1, & διαγράφονται τα: Χ24, Χ34, Χ12, Χ13, Χ15, Χ16.
Χ25 = Χ26 = 1, & διαγράφονται τα: Χ22, Χ23.
Και τέλος, Χ32 = Χ33 = 1, & διαγράφονται τα: Χ35, Χ36.
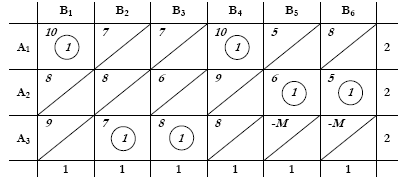
Η απόδοση της αρχικής λύσης είναι: 10 +10 +6 +5 +7 +8 = 46.
ΒΕΛΤΙΣΤΗ ΛΥΣΗ – ΜΕΘΟΔΟΣ STEPPING-STONE
Λόγω των περιορισμών, η αρχική λύση έχει μόνο 6 β.μ. ενώ θα έπρεπε να έχει m+n-1=8 ανεξάρτητες βασικές μεταβλητές. Για να μπορούμε να προχωρήσουμε στη λύση, προσθέτουμε 2 ακόμη μεταβλητές στη βάση δίνοντας τους μια πολύ μικρή τιμή ε ώστε να μην επηρεάζουν το αποτέλεσμα. Επιλέγουμε δυο ανεξάρτητες μη β.μ., τις Χ21 = Χ13 = ε, και διορθώνουμε ανάλογα και τα αi, βj.
Μπορούμε τώρα να βρούμε για όλες τις μη β.μ. την οριακή επίδραση τους στην απόδοση αν αυξηθούν κατά 1 μονάδα: d12 =+7-7+8-7= +1, d15 =+5-10+8-6= -3, d16 =+8-10+8-5= +1, d22 =+8-8+10-7+8-7= +4, d23 =+6-7+10-8= +1, d24 = +9-10+10-8= +1, d31 = +9-8+7-10 = -2, d34 =+8-10+7-8= -3. Από τις 4 θετικές τιμές διαλέγουμε την μεγαλύτερη δηλ. αυτή που θα αυξάνει περισσότερο την απόδοση: d22=+4.

Κάνουμε το Χ22 = min{1, ε} = ε, και προσαρμόζουμε ανάλογα τις υπόλοιπες β.μ. του βρόγχου.
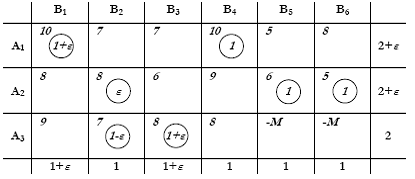
Στη νέα αυτή λύση οι β.μ. είναι πάλι λιγότερες (7 αντί 8) οπότε πρέπει να προσθέσουμε άλλη μια ανεξάρτητη μεταβλητή στη βάση δίνοντάς της μια πολύ μικρή τιμή ε. Επιλέγουμε να κάνουμε τη Χ16 = ε και διορθώνουμε αντίστοιχα τα τα αi, βj. Στη συνέχεια βρίσκουμε πάλι για όλες τις μη β.μ. την οριακή επίδραση τους στην απόδοση αν αυξηθούν κατά 1 μονάδα:
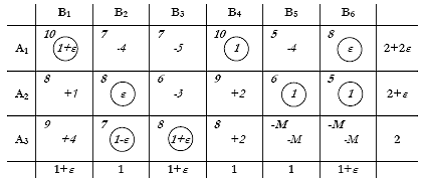
Από τις 4 θετικές τιμές διαλέγουμε την μεγαλύτερη: d31=+4. Κάνουμε το Χ31 = min{1-ε, 1+ε} = 1-ε, και προσαρμόζουμε ανάλογα τις υπόλοιπες β.μ. του βρόγχου. Στη νέα αυτή λύση βρίσκουμε πάλι για όλες τις μη β.μ. την οριακή επίδραση τους στην απόδοση αν αυξηθούν κατά 1 μονάδα:

Από τις 2 θετικές τιμές διαλέγουμε την μεγαλύτερη: d24=+2. Κάνουμε το Χ24 = min{1, ε} = ε, και προσαρμόζουμε ανάλογα τις υπόλοιπες β.μ. του βρόγχου. Στη νέα αυτή λύση βρίσκουμε πάλι για όλες τις μη β.μ. την οριακή επίδραση τους στην απόδοση αν αυξηθούν κατά 1 μονάδα:
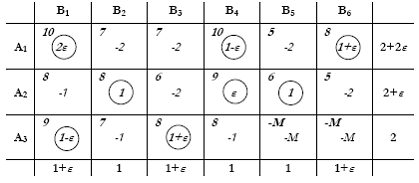
Εφόσον δεν υπάρχουν θετικές οριακές αποδώσεις, η λύση είναι η βέλτιστη.
Η απόδοσή της θα είναι (αγνοούμε τα ε): 10+8+8+6+9+8 = 49, μεγαλύτερη της αρχικής.
Η παραπάνω λύση του προβλήματος κατανομής σημαίνει ότι στο φορτωτή θα εργαστούν οι Β4 & Β6, στον γαιοπροωθητή (bulldozer) θα εργαστούν οι Β2 & Β5, και στον γαιοδιαμορφωτή (grader) θα εργαστούν οι Β1 & Β3. Επιπλέον για καλύτερη συνεργασία οι χειριστές από κάθε ζευγάρι με την μεγαλύτερη απόδοση (Β4, Β2, & Β1) τοποθετούνται στην ίδια βάρδια και οι άλλοι (Β6, Β5, & Β3) στην άλλη βάρδια.

